시계열 분석 시리즈 (1): 정상성 (Stationarity) 뽀개기

Posted on 2021-08-08 Edited on 2023-05-20 In statistics

이번 포스팅은 실전 시계열 분석: 통계와 머신러닝을 활용한 예측 기법 책과 Forecasting: Principles and Practice책을 기반으로 정상성에 대해 자세하게 정리하였습니다.

이번 포스팅은 실전 시계열 분석: 통계와 머신러닝을 활용한 예측 기법 책과 Forecasting: Principles and Practice책을 기반으로 정상성에 대해 자세하게 정리하였습니다.

정상성: 통계적 시계열 분석에 필요한 가정

시계열 자료를 분석하는 통계적인 방법에서 빠질 수 없는 개념은 **정상성 (Stationarity)**입니다. 그 이유는 정상성은 시계열 분석을 할 때 필수적으로 고려하는 가정이기 때문이죠.
마치 회귀 분석을 할 때 오차의 정규성, 등분산성을 만족해야 그 회귀 분석 결과를 믿을 수 있는 것처럼, 시계열 분석을 할 때에도 정상성을 만족해야 분석 결과에 대해 신뢰할 수 있습니다.

그러나 실제로 시계열 분석을 할 때 정상성이 왜 필요한지도 모르겠고, 어떻게 해야 정상성을 만족시킬 수 있는지, 어떻게 해야 정상성을 띤다고 말할 수 있는지 애매할 때가 있습니다.
따라서, 이 포스트를 통해서

정상성을 먼저 정의하고,
정상성을 만족시킬 수 있는 방법인 차분과 로그 변환에 대해 설명하고
정상성을 만족시키는지 파악하기 위한 방법으로
- 그래프를 통해 직관적으로 파악하는 방법과
- 통계적 검정을 이용해 확인하는 방법을 소개하겠습니다.

정상성의 정의

정상성 (定常性)은 "안정되다"라는 뜻을 가진 정 (定)과 "항상"이라는 뜻을 가진 상 (常)의 한자를 가져, "일정하여 늘 한곁같은 성질"을 의미합니다. 이 단어 뜻에 맞게
정상성을 가진 시계열은 과거와 현재와 미래의 모두 항상 안정적인, 일정한 분포를 가진 것이 특징입니다.

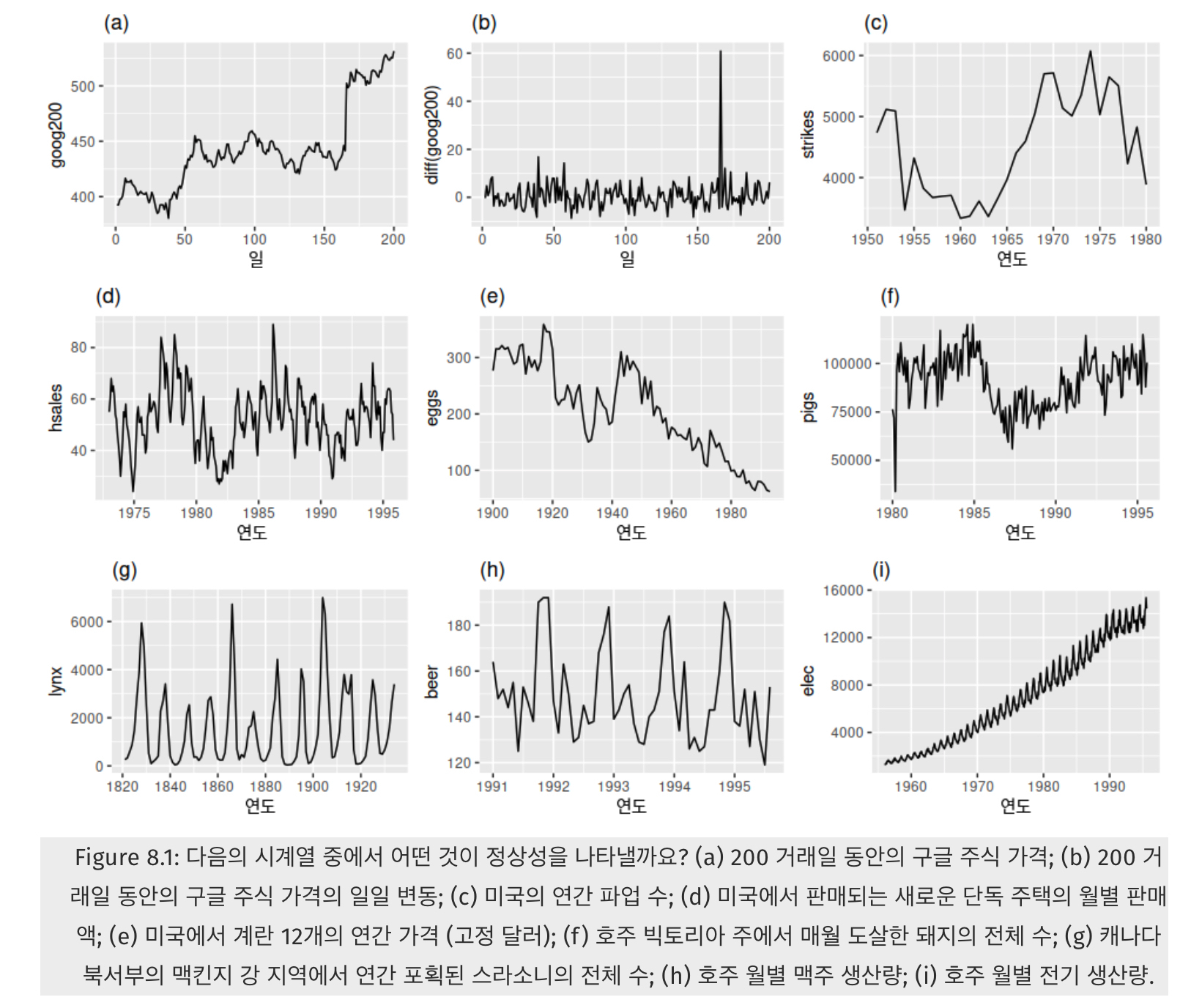
여기서 정상성을 가지는 시계열은 (b)와 (g)뿐입니다.
{:.figure}

정상성을 가진 시계열을 직관적으로 파악하려면, 연필을 들고 지그재그 모양을 수평으로 막 그리면 그게 바로 정상성입니다! 위 그림에서 보면 (b)와 (g)가 그에 해당합니다.

(d),(h)는 계절성이 보이기 때문에 정상성을 띠지 않습니다.
(a),©,(e),(f)는 어떤 특정한 트렌드 (추세)가 있기 때문에 정상성을 띠지 않습니다.
(i)는 계절성도, 트렌드도 보이며 심지어 분산도 시간에 따라 커지는 형태이므로 정상성을 띠지 않습니다.

결과적으로 정상성은 어떤 특정한 주기로 반복하는 계절성이나 위로 혹은 아래로 가는 트렌드가 없어야 하며, 분산도 커지면 안되는 것이라 유추 할 수 있습니다. 즉, 시간에 무관하게 과거, 현재, 미래의 분포가 같아야 한다는 의미입니다.

그렇다면, 정상성 (Stationarity)을 더 엄밀히 정의해봅시다.

정상성이란 시계열의 평균과 분산이 일정하고, 특정한 트렌드 (추세)가 존재하지 않는 성질을 의미합니다.

정상성은 강한 정상성 (Strong Stationarity)와 약한 정상성 (Weak Stationarity)로 정의가 되는데, 일반적으로 약한 정상성만 만족해도 분석이 타당하다고 보기 때문에,
약한 정상성에 대해서만 더 자세히 알아보겠습니다.

약한 정상성을 수학적으로 더 엄밀하게 정의한다면 다음의 세 가지 조건을 만족해야 합니다.

임의의 $t$ 에 대해서 $E(X_t) = \mu$
임의의 $t$ 에 대해서 $Var(X_t) < \infty$
임의의 $t$ , $h$ 에 대하여 $Cov(X_{t+h}, X_t) = \gamma(h)$

3번에서 $\gamma(h)$ 는 자기공분산 함수 (Autocovariance Function, ACVF)라 불리우는데, 공분산이 시점 $t$ 에 의존하지 않고, 시간의 차이인 $h$ 에만 의존함을 의미합니다.

예를 들어, A 주식이 정상성을 띤다고 가정합시다.
이 주가의 평균이 3천원이고, 임의의 시점을 $t$ = 2020년 1월 3일이라 치면

1. 2020년 1월 3일의 주가의 평균이 $\mu = 3천 원$ 이고
1. 2020년 1월 3일의 주가의 분산이 유한하며 (= 극단치로 터지지 않고)
1. 2020년 1월 3일의 주가와, 그로부터 5일 뒤인 2020년 1월 8일의 주가 간의 공분산이 $\gamma(5)$ 임을 의미합니다.

정상성이 중요한 이유

정상성이 중요한 이유는 시계열의 평균과 분산이 일정해야 시계열 값을 예측할 수 있기 때문입니다.
시계열 분석에서는 "우리가 구한 시계열 자료"가 어떤 시간에 따른 **확률 과정 (stochastic process)**에서 실현된 값이라고 보는데요.

확률 과정이라는 말이 어려우니 조금 더 익숙한 개념으로 돌아가봅시다. 고등학교 수학에서 확률을 배울 때

\bar{X} \sim N(\mu, \sigma^2 /n)

인 성질을 이용해서 신뢰 구간도 구하고, 가설 검정도 했던 것을 기억하시나요?

여기서 $\bar{X}$ 는 우리가 얻은 $n$ 개의 데이터 (= 표본, samples) $X_1,X_2,\ldots,X_n$ 의 평균, 즉 표본 평균이고, $\mu$ 는 모 평균, $\sigma^2$ 은 모 분산에 해당합니다.
이는 표본들의 평균이 일정한 평균과 분산을 가지는 정규분포를 따른다는 의미이죠.

여기서 확장되어 확률 과정은 시간별로 표시된 확률 변수의 집합으로 정의가 됩니다. 즉, 각 시점 $t$ 에서의 값이 확률 분포 (예컨대, 위 예시처럼 각 시점에서의 값 (주가, 임금 등 우리가 관심있는 값) 이 정규분포를 따르는 것이죠)를 따른다고 보고, 이를 종합적으로 고려했을 때 시간 $t \in [0,\infty]$ 에서의 값들이 어떤 확률 분포를 따를 때 확률 과정이라 부를 수 있습니다.

그런데, 우리가 얻은 데이터 (= 표본)에 대응되는 것이 우리가 얻은 시계열 자료이고, 이들은 일정한 평균과 분산을 가진 확률 과정 (stochastic process)을 따른다고 가정해야만 시계열 예측을 할 수 있습니다. 가령, 오늘의 주가가 3000원인데, 이 주가는 이상적인 천상의 주가 그래프에서 여러 개를 표본 선출하여 만든 수치들 (Ex. 2000원, 2500원, 5000원, …, 3000원)의 평균 값이라고 볼 수 있는 것이죠.

만약 시간의 흐름에 따라서 이 확률 분포가 크게 변동한다면, 그 실현값들의 평균이나 분산 등 모멘트가 의미가 없기 때문에 적어도 이 평균과 분산이 우리가 다루고자 하는 확률 과정을 설명하기에 문제가 없도록 하기 위해 필요한 조건이 바로 정상성입니다.

결과적으로 정상성을 띄는 확률 과정을 그림으로 표현하면 다음과 같습니다.

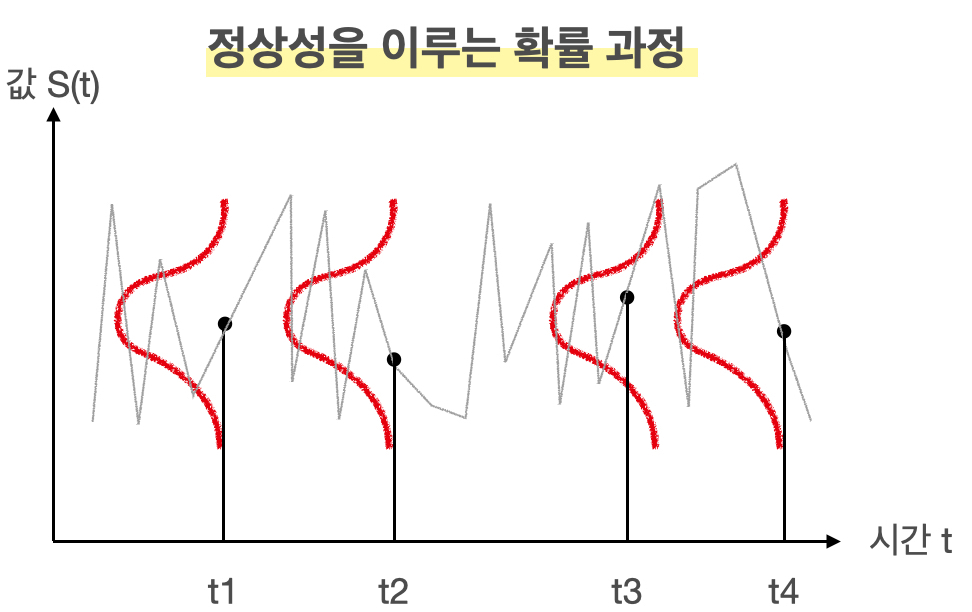
회색 선이 시계열 자료라면, 빨간색 선처럼 각 시점에서 확률 분포를 가지고, 이들의 평균과 분산이 동일한 분포이므로 확률 과정이 정상성을 띤다 볼 수 있습니다.

정상성을 만족시키기 위한 두 가지 방법

보통 시계열 자료는 정상성을 띠지 않는 자료가 많습니다. 생각해보면 주가도 시간에 따라 증가하는 모습을 보이고, 분산도 언제는 작았다가 언제는 크기도 하기 때문에 정상성을 띠지 않는게 대부분이죠.

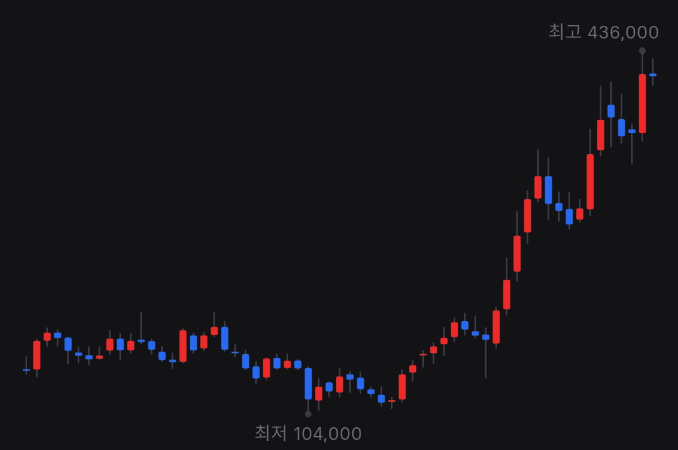
위 그림은 네이버 주가의 월봉 그래프로, 평균이 일정하지 않고 올라가는 추세를 보이고, 월마다 변하는 정도도 제각각인 것을 보아 분산도 다름을 유추할 수 있습니다. 즉, 정상성을 띠지 않습니다.

이렇게 시계열 자료가 정상성을 띠지 않으면, AR, MA, ARIMA 등 전통적인 시계열 분석 방법들을 사용하기 어렵기 때문에 시계열 자료들에 어떤 변환을 취해 정상성을 띠도록 만들어야 합니다.
바로 **차분 (Differencing)**과 로그 변환입니다.

차분 (Differencing)

차분은 $t$ 시점과 $t-1$ 시점의 값의 차이를 구하는 것을 의미합니다.

여기서 정상성을 가지는 시계열은 (b)와 (g)뿐입니다.
{:.figure}

다시 위 그림에서 (a)의 구글의 주식 가격이 정상성을 나타내는 시계열이 아니었지만, (b)는 구글의 주식 가격의 일별 변화는 정상성을 나타냈다는 것을 주목합시다. 즉, 연이은 관측값의 차이를 계산하는 차분을 취하면, 그 차이값들의 평균은 일정하기 때문에 정상성을 띠게 되는 것입니다.

차분을 수식을 통해 정의하면 다음과 같습니다.

\Delta y_t = y_t - y_{t-1}

첫 번째 관측값에 대한 차분 $\Delta y_1$ 을 구할 수 없기 때문에, 차분값들은 $T-1$ 개의 값만 가지게 됩니다.

2차 차분

가끔 차분을 해도 시계열의 정상성이 만족되지 않는 경우도 있습니다. 그럴 경우, 정상성을 나타내는 시계열을 얻기 위해 다음과 같이 한 번 더 차분을 구하는 작업이 필요할 수도 있습니다.

\begin{aligned} \Delta y_t - \Delta y_{t-1} &= (y_t - y_{t-1}) - (y_{t-1} - y_{t-2})\\ & = y_t - 2y_{t-1} + y_{t-2} \end{aligned}

이 경우 2차 차분값은 $T-2$ 개의 값을 가지게 됩니다. 결국, 2차 차분은 원본 시계열 데이터의 "변화에서 나타나는 변화"를 모델링하게 되는 셈입니다. 실제 상황에서는 2차 차분 이상으로 구하는 경우는 거의 일어나지 않는다 합니다.

계절성 차분

계절성 차분은 관측치와, 같은 계절의 이전 관측값과의 차이를 말합니다. 따라서 다음과 같이 정의가 됩니다.

y_{t} - y_{t-m}

여기서 $m$ 은 주기에 해당합니다. 즉 $m=12$ 이고 월별로 집계된 값이라면, 올해 1월의 값 - 작년 1월의 값, 올해 2월의 값 - 작년 2월의 값, … 이 되겠죠.

로그 변환

로그 변환을 통해 정상성을 띠지 않는 시계열 자료의 분산을 줄일 수 있습니다.

정상성을 만족시키는 두 번째 방법으로 로그 변환을 고려할 수 있습니다. 말 그대로 값에 시계열 값에 로그를 취하면 됩니다.

y_t \rightarrow \log (y_t)

로그 변환은 특히 값의 변동 자체가 큰 경우 (= 분산이 큰 경우) 고려할 수 있는 방법입니다. 또한, GDP와 같은 많은 경제 시게열 자료가 근사적으로 지수적인 성장을 나타내고 있는 경우가 많기 때문에 이런 시계열 자료에 로그를 취해 선형적인 값으로 바꿔주는 효과 또한 있습니다.

그러나, 로그 변환을 통해 어떤 시계열 자료가 선형적인 추세를 보인다면 시간이 지남에 따라 평균이 일정하지 않고 증가한다는 뜻이기 때문에, 이 또한 정상성을 띠지 않는 문제가 있습니다.
그럼 뭐야? 라고 생각이 들겠지만 다음 장에서 그 해답을 찾을 수 있습니다.

로그 변환 + 차분 (로그 차분)

그래서 저희는 PPAP 전법이 필요합니다. 즉,

로그 변환을 통해서 먼저 분산을 안정화시키고, 지수적인 값을 가지는 시계열을 선형적으로 바꿔준 다음,
로그 변환된 시계열 값에 차분을 취해 정상성을 만족시키도록 만드는 것입니다.

시간에 따라 어떤 시계열이 선형적으로 증가한다는 뜻은 즉, 그 시간에 따른 증가분 (차분)이 일정하다는 것이기 때문에, 로그 변환된 시계열에 차분까지 해주면 정상성을 만족시킬 수 있는 것입니다.

더 놀라운 것은 로그의 차분값이 증가율의 근사값이라는 것이 알려져 있습니다.
즉, 저희가 PPAP 전법을 통해 로그의 차분값을 다음과 같이 정의한다면,

\Delta \log(y_t) = \log y_t - \log y_{t-1}

이 값을 $y_{t-1}$ 에서 $y_t$ 로의 증가율로 근사할 수 있습니다.

\Delta \log(y_t) = \log y_t - \log y_{t-1} \simeq \frac{y_t - y_{t-1}}{y_{t-1}}

왜 놀랍냐면, 해석 상 이점이 있기 때문입니다. 가령 "GDP의 로그의 차분값이 AR (1)과정을 따릅니다"라는 말보다 "GDP의 증가율이 AR(1) 과정을 따릅니다"가 직관적으로 잘 와닿지 않나요?

실제 경제 지수에서 이를 잘 설명하는 지표는 소비자 물가 지수 (CPI; Customer Price Index)입니다.

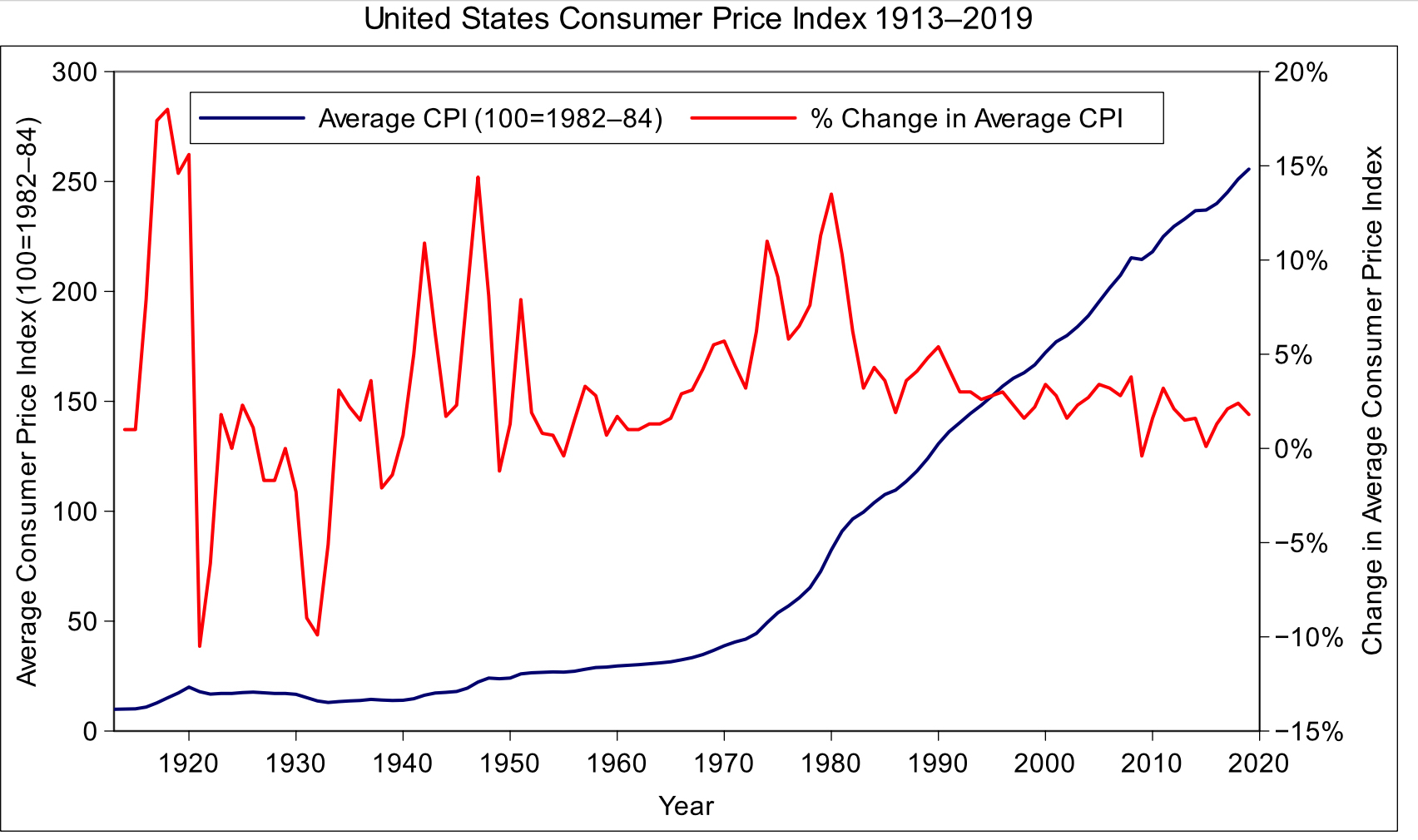
미국의 CPI와 CPI 변화율, 출처: [link]
{:.figure}

위 그림에서 보면 파란색 선이 CPI, 빨간색 선이 CPI의 변화율을 나타냅니다. CPI는 장기적으로 봤을 때 매우 강한 장기 추세를 가집니다. 이에 비해 변화율은 CPI보다는 어떤 추세를 보이고 있지 않습니다.

\frac{CPI_{t} -CPI_{t-1}}{CPI_{t-1}}

로 정의가 됩니다. 즉, 이 값은 로그 차분값과 비슷하기 때문에

\frac{CPI_{t} -CPI_{t-1}}{CPI_{t-1}} \simeq \Delta \log (CPI_{t})

로 간주할 수 있습니다. 그러나 이 값도 분산으로 보면 과거에는 분산이 매우 컸으나, 현재 와서는 또 분산이 안정적으로 보이고 있어서 정상성을 띠고 있다고 보기 어렵습니다.

"PPAP 전법이 통하지 않는데, 그럼 어떡하냐"하신다면 대답해드리는게 인지 상정!
정답은 로그 차분값에 또 차분을 할 수 있습니다 (즉 2차 차분을 시행합니다).

CPI의 연 변화율은 인플레이션율과 같은 의미인데, 이 인플레이션율의 연간 차이를 구하면 정말 정상성을 띠게 됩니다. 즉, 수식으로 표현하면 $\Delta Inf_{t}$ 가 정상성을 띠게 됩니다.

\begin{aligned} Inf_t &= \frac{CPI_{t} -CPI_{t-1}}{CPI_{t-1}} \simeq \Delta \log (CPI_{t})\\ \Delta Inf_t &= Inf_t - Inf_{t-1}\\ \end{aligned}

정상성 검증을 위한 두 가지 방법

휴, 정상성을 띠도록 하는 두 가지 방법에 대해 알아보았는데요.
이렇게 차분 또는 로그 변환을 통해 시계열을 "안정화"시켜줬을 때 실제로 그 변환된 시계열이 정상성을 만족하는지 검증하는 과정이 필요합니다.
크게 그래프로 직관적으로 파악하는 방법과 혹은 통계적인 검정 방법을 이용하여 정상성을 검증할 수 있습니다.

그래프로 정상성 파악하기

그래프 상 추세가 없이 일정한 폭으로 상승과 하락을 반복한다면 정상성을 띠는 그래프라 추측할 수 있습니다. 또한, ACF가 허용 범위 안에 존재한다면 정상성을 띤다 말할 수 있습니다.

위에서 정상성의 정의를 내렸을 때 아래 그래프를 활용한 것을 기억하시나요?

여기서 정상성을 가지는 시계열은 (b)와 (g)뿐입니다.
{:.figure}

이처럼 시계열의 모습만 보고도 직관적으로 정상성을 띠는지 확인할 수 있습니다. 정상성의 정의에 따라서,

그래프에 지속적인 상승 또는 하락 추세가 없어야 하고
과거의 변동폭과 현재의 변동폭이 같아야 하며
계절성도 없어야 합니다.

또한, 이런 정상성을 가진 시계열은 평균으로 회귀하려는 특징 (Mean reverting)을 가지고 있습니다.
즉, 어떤 시점에서 평균을 크게 벗어났는데 조만간 다시 평균으로 돌아가려는 성향을 가지고 있다면, 정상성을 가진다 추측해볼 수 있습니다.

이보다 더 직관적인 방법은 자기 상관 함수 (ACF; Auto Correlation Function)을 이용하는 것입니다.
자기 상관 함수는 전혀 새로운 개념은 아니고, 일반적인 상관 계수를 구하는 공식에서 X와 Y간의 상관 관계를 구하는 대신, 시계열 자료인 X 자체의 상관 관계를 구하기 위해 고안된 것일 뿐입니다.
즉, 시계열 자료에서 $t$ 시점의 값과 그보다 $k$ 시점 앞선 $t-k$ 시점 간의 상관 계수를 $r_k$ 라 할 때, 다음과 같이 자기 상관 함수가 정의됩니다.

r_k = \frac{\sum_{t = k+1}^T (y_t - \bar{y}) (y_{t-k} - \bar{y})}{\sum_t^T (y_t - \bar{y})^2}

여기서 $T$ 는 시계열 데이터의 행 수를 의미합니다.

수식은 크게 중요하지 않고, ACF를 그렸을 때 어떻게 나와야 정상성이 보이는지 아는 것이 중요합니다.
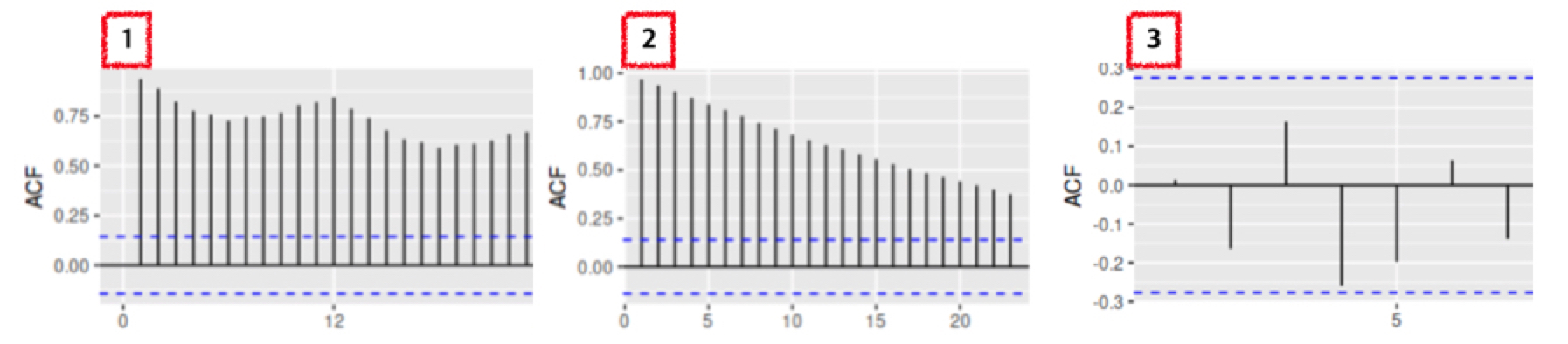
퀴즈입니다! 다음 1 ~ 3번의 ACF 중에 어떤 ACF가 정상성을 띠는 그래프일까요?

방법도 안 알려주고 냅다 퀴즈를 던져 당황하셨죠? 그래도 직감이란 것이 있을 것 같아 말씀드려보았습니다.
정답은 3번 그래프입니다. 3번 그래프와 1, 2번 그래프를 비교했을 때 가장 큰 차이점은 "파란색 점선 안에 값이 들어왔는지"입니다.

ACF 그래프에서 가로축은 시차 (lag), 세로축은 ACF의 값입니다. 예를 들어, 4에 찍힌 값은 $y_t$ 와 네 시점 앞인 $y_{t-4}$ 간의 ACF를 의미합니다.
이 때 1번과 2번은 시차가 뒤로 갈수록 ACF 값이 감소하고 있지만, 확연하게 줄어들지 않습니다.
이는, 오늘의 데이터가 어제의 데이터에 가장 크게 의존하고, 시간이 지날수록 오늘과 먼 과거의 데이터 간의 자기 상관은 감소함을 의미합니다.

이에 비해 정상성을 띠는 데이터는 파란색 점선, 즉 신뢰 구간 안에 자기 상관이 존재합니다. 이럴 경우, 데이터가 정상성을 띤다고 할 수 있습니다.
즉, 어제의 데이터와 오늘의 데이터 간에 상관 관계는 당연히 있겠지만, 허용 범위 (파란색 점선) 안에 들어온다는 것을 의미합니다.

가설 검정으로 정상성 파악하기

귀무 가설을 기각해야 (p-value가 작아야) 정상성을 띱니다!

정상성을 파악하는 두 번째 방법은 가설 검정입니다. 바로 단위근 검정 (Unit Root Test)인데요.
이 검정에는 여러 학자들이 고안하여 검정 방법이 아래와 같이 존재합니다.

KPSS 검정
Dicky-Fuller 검정
ADF 검정 (Augmented Dicky-Fuller Test)

설명의 편의성을 위해, AR(1)모형에서의 Dicky-Fuller Test에 대해 설명드리겠습니다.

AR(1) 모형은 아직 설명하지 못했지만 현 시점의 값이 한 시점 앞의 시점 (lag = 1)의 값에 의존하는 모형으로, 다음과 같이 쓸 수 있습니다.

y_t = \beta_0 + \beta_1 y_{t-1} + e_t

여기서의 귀무 가설과 대립 가설은

H_0 = \beta_1 = 1\ vs. \ H_1: \beta_1 < 1

로 정의가 되는데요.
귀무 가설을 만족한다면 $\beta_1 = 1$ 이고, 이 때의 모형은 $y_t = \beta_0 + y_{t-1} + e_t$ 가 됩니다.

이런 모형이 어떻게 생겼는지 아래 두 모형으로 간단하게 시뮬레이션을 해보겠습니다.

모형 1: $\beta_0 = 3, \beta_1 = 1 \rightarrow y_t = 3 + y_{t-1} + e_t$
모형 2: $\beta_0 = 3, \beta_1 = 0.1 \rightarrow z_t = 3+ 0.1z_{t-1} + e_t$

import numpy as np
import matplotlib.pyplot as plt
init = np.random.normal(size=1, loc = 3)
e = np.random.normal(size=1000, scale = 3)

y = np.zeros(1000)
z = np.zeros(1000)
y[0] = init
z[0] = init

for t in range(1,1000):
    y[t] = 3 + 1 * y[t-1] + e[t] # beta1 = 1 단위근 모형
    z[t] = 3 + 0.1*z[t-1] + e[t] # beta1 = 0.1

fig,ax = plt.subplots(1,2)
ax[0].plot(y)
ax[0].set_title("Non-Stationary")
ax[1].plot(z)
ax[1].set_title("Stationary")
plt.show()

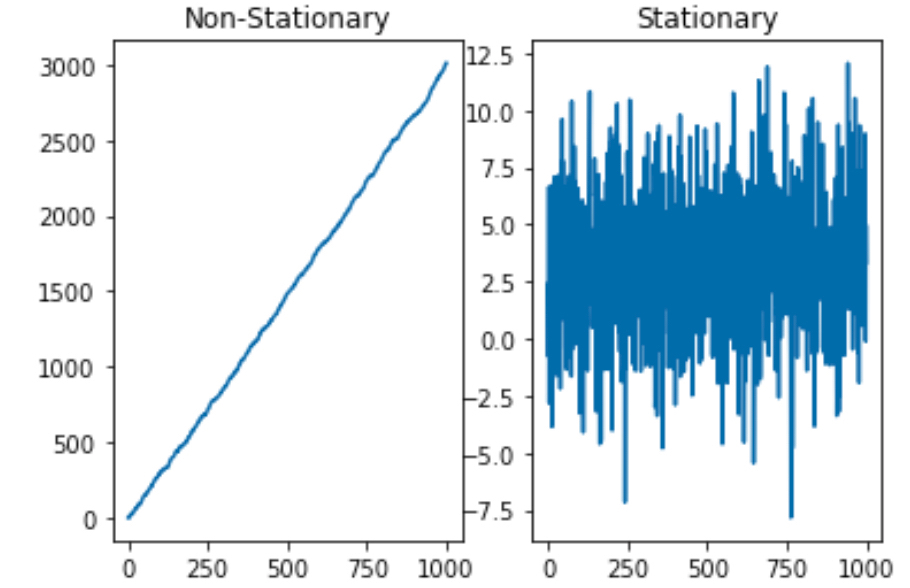
그래프로 판단해봤을 때, $y_t$ 는 아주 강력한 상승 추세를 가지기 때문에 정상성을 띠지 않지만, $z_t$ 는 정상성을 띠는 듯합니다.

이처럼 $\beta_1 = 1$ 이면 단위근을 가졌다고 하고, 이 단위근을 가진 AR 모형 $y_t$ 은 정상성을 띠지 않습니다.
따라서 귀무 가설 $\beta_1 = 1$ 을 기각해야 정상성을 띤다 말할 수 있습니다.

그런데 말입니다. 단위근은 어디서 나온 단어일까요?

AR(p) 모형 (시차 = p까지 설명이 되는 모형)이 정상성을 띠기 위한 조건은 특성 방정식의 모든 근의 절대값이 1보다 커야 한다는 것입니다.
특성 방정식은 다음과 같이 쓸 수 있습니다.

1-\beta_1B -\beta_2 B^2 -\cdots - \beta_p B^p = 0

여기서 B는 후방 이동 (backshift) 연산자로, 시계열의 시차를 다룰 때 쓰는 표기법입니다. 즉, 아래와 같이 말이죠!

\begin{aligned} B y_t &= y_{t-1}\\ B^2 y_t &= y_{t-2}\\ \vdots \end{aligned}

만약 이 특성방정식의 근이 1인 것을 가지고 있다면 이 때 단위근을 가지고 있다고 말합니다.
$y_t = y_{t-1} + e_t$ 모형으로 특성 방정식과 그 근을 구해봅시다.
이 모형은 $\beta_1 = 1$ 인 AR(1)모형으로 **확률 보행 모형 (random walk model)**이라 부릅니다.
이 모형에 후방 이동 연산자를 적용하고, 에러 $e_t$ 에 대해 식을 정리한다면 특성 방정식의 해를 구할 수 있습니다.

\begin{aligned} y_t &= By_t + e_t\\ e_t &= y_t - By_t\\ e_t &= (1-B)y_t \end{aligned}

여기서의 특성 방정식은 $(1-B) = 0$ 이 되어 해가 $B=1$ 로 계산이 됩니다.
그래서 이 모형은 단위근을 갖게 되고, 정상성을 가지지 않는 대표적인 모형입니다.

실전! 삼성 전자 주가 정상성을 띠도록 만들기!

수식이 중요한가요? (~~중요할 때도 있음(…)~~)
결과적으로 데이터가 정상성을 띠는지, 띠지 않는다면 정상성을 띠도록 만들어 주는게 핵심입니다.

따라서 이 파트에서는 실제 삼성전자의 주가를 가지고 차분 및 로그 변환을 했을 때 정상성을 만족하는지 검정해보도록 하겠습니다.
이를 위해 파이썬에서 다음과 같이 데이터를 로드합니다.

import FinanceDataReader as fdr
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import plotly.graph_objects as go

# 한국거래소 상장종목 전체
df_krx = fdr.StockListing('KRX')
# 삼성 티커
ss_ticker = df_krx[df_krx.Name=='삼성전자']['Symbol'] 
print(ss_ticker) #005930

FinanceDataReader는 한국 주식 가격, 미국주식 가격, 지수, 환율, 암호화폐 가격, 종목 리스팅 등 금융 데이터 수집 라이브러리입니다. ([link])
이 곳에서 KRX에 상장된 모든 주식을 확인할 수 있는데, 삼성 전자의 주식 데이터를 불러오기 위해 삼성 전자의 티커^{Ticker, 주식 종목명을 쉽게 찾을 수 있는 코드} 005930를 찾았습니다.

이제 삼성 전자의 티커와, 시작 날짜와 끝 날짜를 지정하여 삼성 전자의 주식 자료를 불러오겠습니다.

1 2	ss = fdr.DataReader('005930','2015-01-01', '2021-07-31') ss.tail()

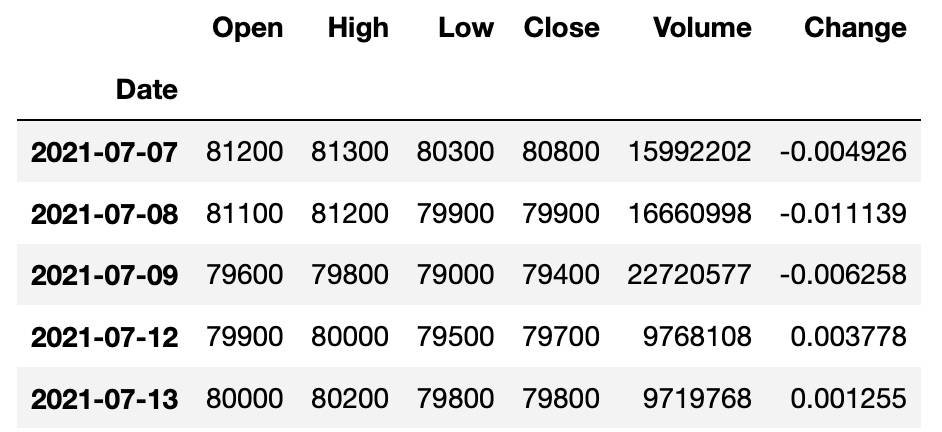
주식을 하는 분이라면 다 아시겠지만, 위 데이터는 일별로 주식 거래량을 집계한 정보로 컬럼에 대한 설명은 다음과 같습니다.

Close: 종가 ^{주식 시장이 마감했을 때의 가격}
Open: 시가 ^{주식 시장이 시작했을 때의 가격}
High: 최고가
Low: 최저가
Volume: 거래량
Change: 증감률^{어제 종가 대비 오늘 종가의 증감률}

이 컬럼 정보를 가지고 아래와 같이 손쉽게 봉 차트 (Candle Chart)를 그릴 수 있습니다. 이 봉 차트는 상자 그림과 비슷하지만, 담고 있는 정보가 약간은 다르죠! (저희는 양봉을 마주해야 좋습니다 :>)

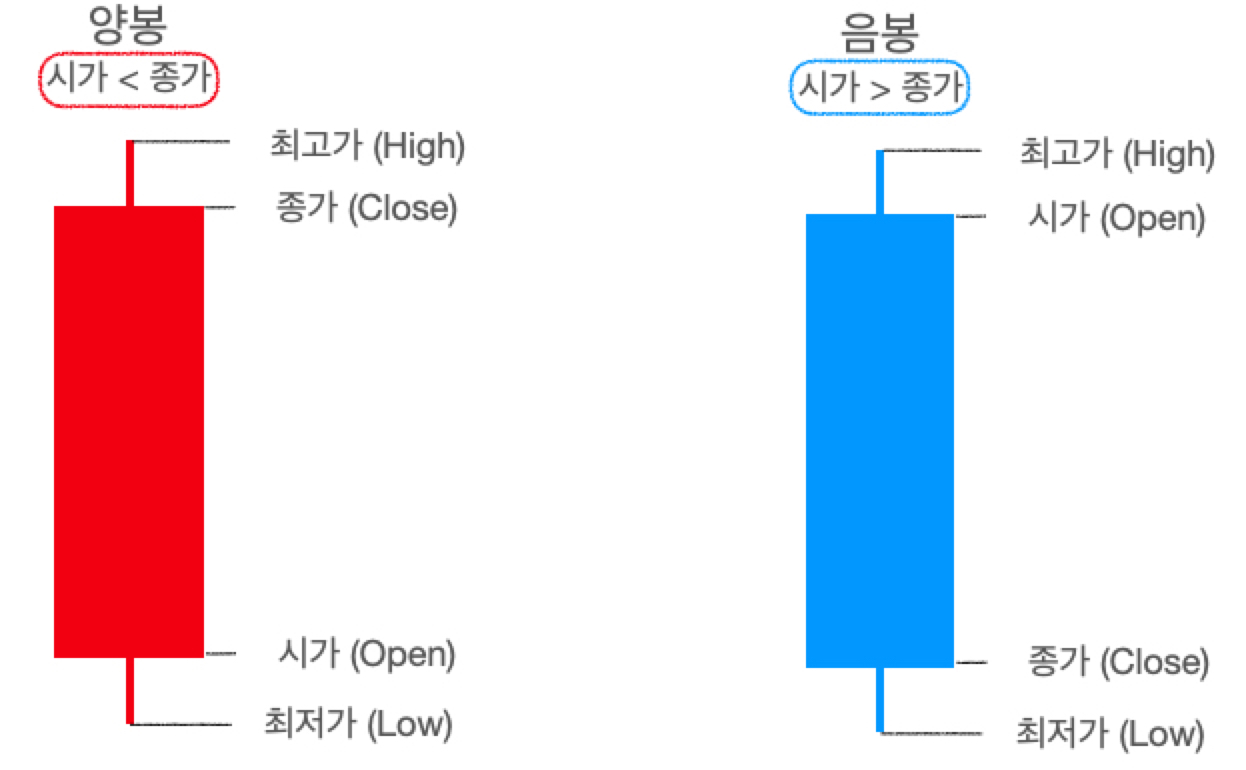
다시 본론으로 들어와서 삼성 전자의 봉 차트를 그리면 이런 우상향하는 모습을 볼 수 있습니다.

ss_candlestick = go.Candlestick(x=ss.index
                   ,open = ss.Open
                   ,high = ss.High
                   ,low = ss.Low
                   ,close= ss.Close)
layout = go.Layout(title = '삼성전자 캔들차트')
go.Figure(data = [ss_candlestick], layout = layout)

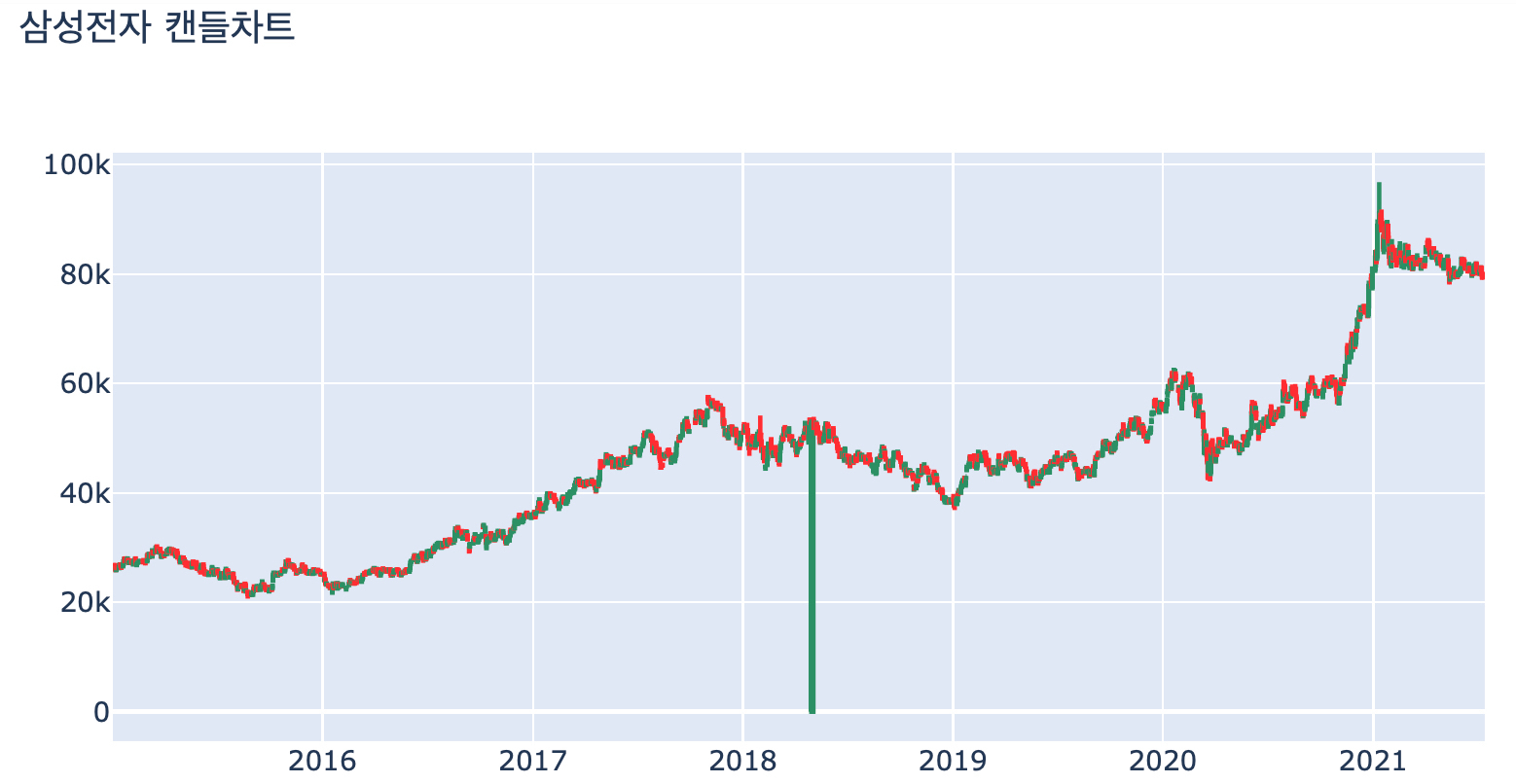
우상향하면 뭐다? 트렌드가 존재한다는 의미이므로, 정상성을 만족하지 않는다 추측할 수 있습니다.
따라서 정상성을 만족시키기 위해 삼성 주가의 종가 (Close)에 차분과 로그 변환, 그리고 로그 차분 (로그 변환 후 차분)을 시도해봅니다.

# 차분
ss['diff_close'] = ss['Close'].diff(1)
# 로그
ss['log_close'] = np.log(ss['Close'])
# 로그차분
ss['logdiff_close'] = np.log(ss['Close']).diff(1)

from plotly.subplots import make_subplots
import plotly.graph_objects as go

fig = make_subplots(4,1)

fig.add_trace(go.Scatter(x=ss.index, y=ss.Close,name = "삼성 주가"),row=1,col=1)
fig.add_trace(go.Scatter(x=ss.index, y=ss.diff_close,name = "삼성 주가 차분값"), row=2,col=1)
fig.add_trace(go.Scatter(x=ss.index, y=ss.log_close,name = "log(삼성 주가)"), row=3,col=1)
fig.add_trace(go.Scatter(x=ss.index, y=ss.logdiff_close,name = "log(삼성주가) 차분값"), row=4,col=1)

fig.update_layout(height=600, width=800, title_text="삼성 주가")
fig.show()

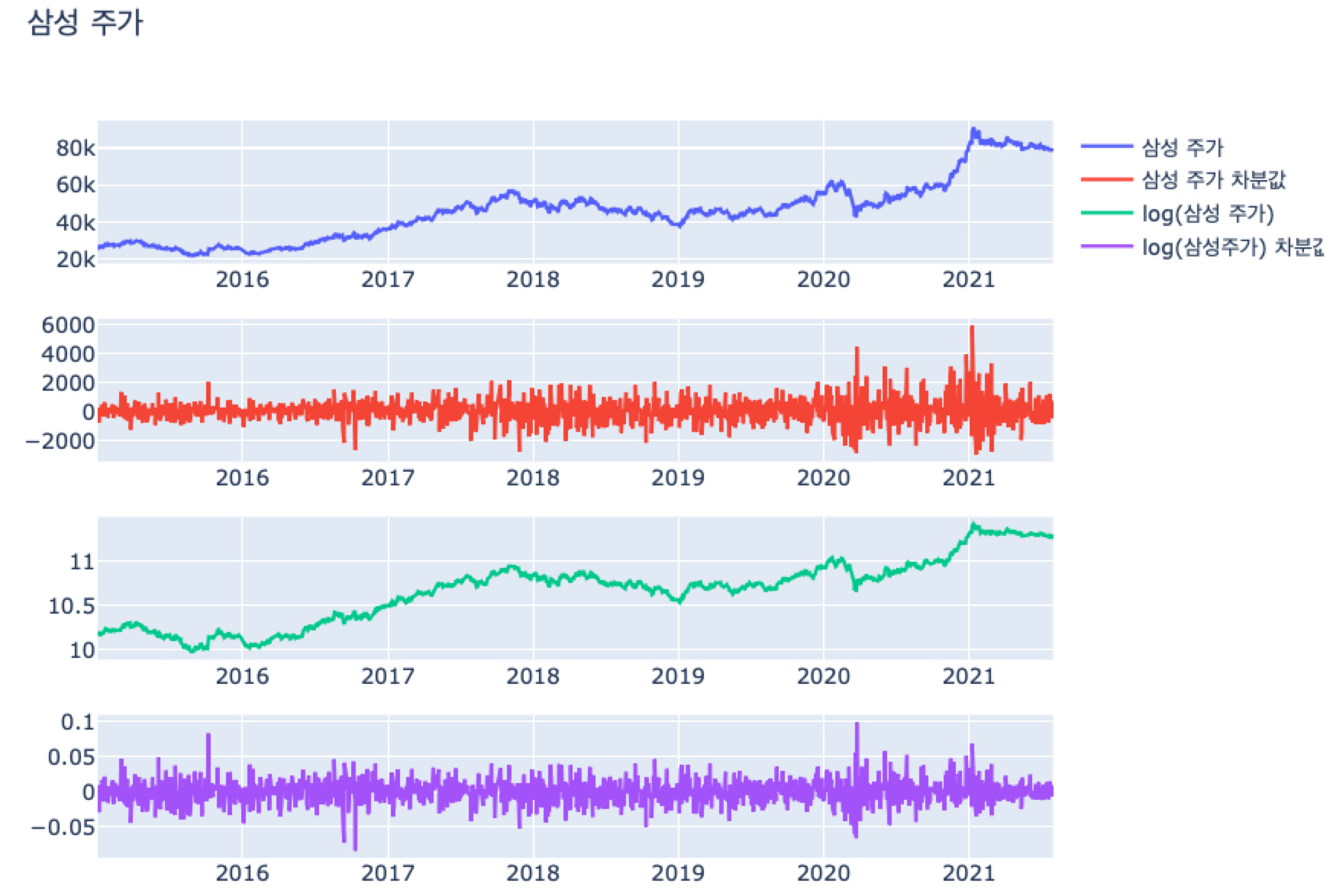
위 그림에서 보면 삼성 주가에서 차분을 하면 그래프가 0을 부근으로 위 아래로 왔다갔다하는 평균 회귀 (Mean Reverting) 성질을 지닙니다.
그러나 과거에는 상승 감소 폭이 $\pm$ 2000이었다면, 현재는 -2000 ~ 6000까지 커졌기 때문에 과거와 현재의 분산이 비슷한지는 약간 애매합니다.
로그 변환을 했더니 여전히 원 그래프처럼 상승하는 트렌드를 보입니다. 대신에 원 그래프는 20,000원 ~ 80,000원으로 상승폭이 크지만, 로그 변환을 하니 10 ~ 11.xx로 분산이 안정화된 것을 알 수 있죠.
PPAP 전법을 통해 로그 차분을 한 그래프는 차분한 그래프에 비해 더 분산이 안정화된 모습을 보입니다.

그럼 이 네 지수 (Close, diff_close, log_close, logdiff_close)의 정상성을 검증해봅시다.

먼저 원 그래프 (왼쪽)와 ACF (오른쪽)를 그리면 다음과 같습니다.

from matplotlib import rc
rc('font', family='AppleGothic')
plt.rcParams['axes.unicode_minus'] = False

fig,ax = plt.subplots(4,2, figsize=(12,16))
ax[0,0].plot(ss['Close'])
ax[0,0].set_title('삼성 주가')
ax[1,0].plot(ss['log_close'])
ax[1,0].set_title('log(삼성주가)')
ax[2,0].plot(ss['diff_close'])
ax[2,0].set_title('삼성 주가 차분값')
ax[3,0].plot(ss['logdiff_close'])
ax[3,0].set_title('log(삼성 주가) 차분값')

plot_acf(ss['Close'],ax=ax[0,1])
plot_acf(ss['log_close'],ax=ax[1,1])
plot_acf(ss['diff_close'][1:],ax=ax[2,1])
plot_acf(ss['logdiff_close'][1:],ax=ax[3,1])

plt.show()

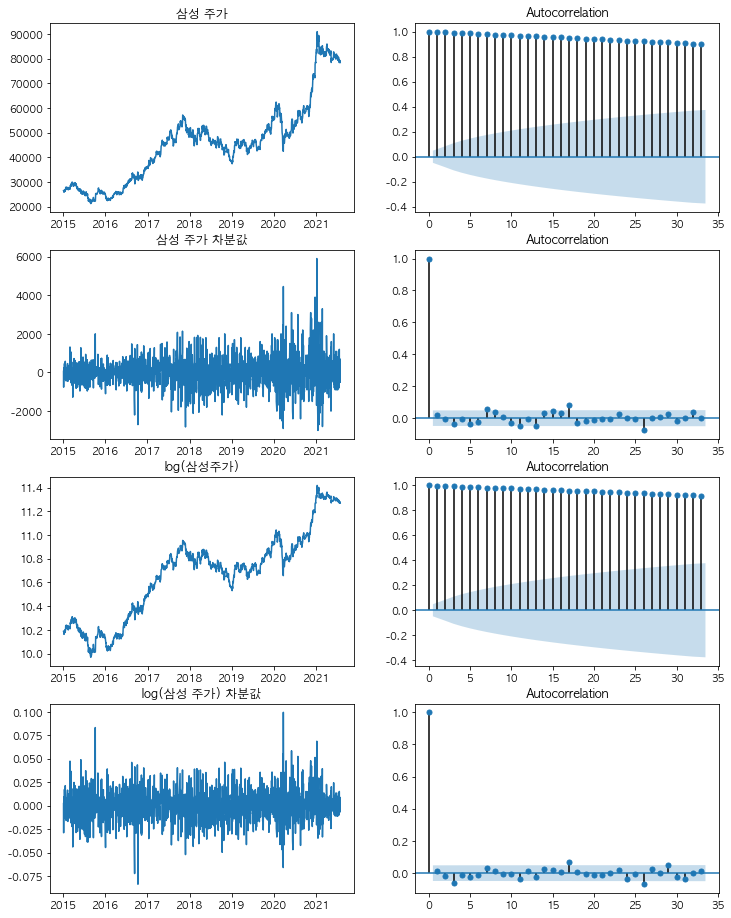
삼성 주가와, 로그 변환을 한 log(삼성 주가)의 ACF는 시간이 지날수록 감소하긴 하지만 아주 더디게 감소하고 있습니다. 시계열 그래프가 선형적으로 증가하는 경우 이러한 그래프를 띠며, 이 때 허용 범위 (파란색 음영) 안에 ACF 값들이 들어오지 않기 때문에 정상성을 띠지 않는다고 볼 수 있습니다.

이에 비해서 삼성 주가 차분값과, log(삼성 주가) 차분값의 ACF는 0인 시점에서 1의 자기 상관을 가지고, lag = 1 이후로부터는 급격하게 자기 상관이 줄어든 것을 확인할 수 있습니다.
몇 군데 (lag = 17, 25) 상에서 허용 범위 밖에 자기 상관이 있긴 하지만, 대부분의 시차에서 자기 상관이 허용 범위 안에 들어와있는 것을 알 수 있습니다.

결과적으로, ACF만 봤을 때 삼성 주가와 log (삼성 주가)는 정상성을 띠지 않을 것이고, 삼성 주가 차분값과 log(삼성 주가) 차분값은 정상성을 띨 것이라 예상할 수 있습니다.

이제, 두 번째 방법인 가설 검정 방법으로 정상성을 검증해보고자 합니다.
파이썬의 adfuller 모듈을 이용하면 ADF 검정 (Augmented Dicky-Fuller Test)을 쉽게 사용할 수 있습니다.

from statsmodels.tsa.stattools import adfuller

def print_adfuller (x):
    result = adfuller(x)
    print(f'ADF Statistic: {result[0]:.3f}')
    print(f'p-value: {result[1]:.3f}')
    print('Critical Values:')
    for key, value in result[4].items():
        print('\t%s: %.3f' % (key, value))

print_adfuller(ss['Close']) ## 정상성 만족 X
print("-"*30)
print_adfuller(ss['log_close']) ## 정상성 만족 X
print("-"*30)
print_adfuller(ss['diff_close'][1:]) ## 정상성 만족
print("-"*30)
print_adfuller(ss['logdiff_close'][1:]) ## 정상성 만족
print("-"*30)

[Close]
ADF Statistic: -0.361
p-value: 0.916
Critical Values:
	1%: -3.434
	5%: -2.863
	10%: -2.568
------------------------------
[log_close]
ADF Statistic: -0.643
p-value: 0.861
Critical Values:
	1%: -3.434
	5%: -2.863
	10%: -2.568
------------------------------
[diff_close]
ADF Statistic: -8.736
p-value: 0.000
Critical Values:
	1%: -3.434
	5%: -2.863
	10%: -2.568
------------------------------
[logdiff_close]
ADF Statistic: -24.766
p-value: 0.000
Critical Values:
	1%: -3.434
	5%: -2.863
	10%: -2.568
------------------------------

검정 결과를 보면 삼성 주가 (Close)와 로그 변환을 한 log(삼성 주가) (log_close)의 pvalue는 모두 0.05보다 크기 때문에 귀무가설을 기각하지 못하여, 정상성을 만족하지 못한다 말할 수 있습니다.
이에 비해 삼성 주가 차분값 (diff_close)와 로그 차분값 (logdiff_close)의 pvalue는 거의 0이기 때문에 귀무가설을 기각하여, 정상성을 만족한다고 볼 수 있습니다.
참고로 차분값의 경우 첫 번째 값이 NA이기 때문에 [1:]을 통해 두 번째 값부터 가져와서 ADF 검정을 시행하였습니다.

ADF 검정도 결과적으로 삼성 주가와 log (삼성 주가)는 정상성을 띠지 않고, 삼성 주가 차분값과 log(삼성 주가) 차분값은 정상성을 띤다는 결론을 도출하였습니다.

여담

최근에 삼성 주가가 제자리 걸음 중인데요. 혹시 최근 한 달 간의 주가 자체도 정상성을 띠지 않을까? 하여 ACF를 그려보았습니다.

fig,(ax1,ax2) = plt.subplots(1,2, figsize=(14,4))
ax1.plot(ss['Close'][-30:])
plot_acf(ss['Close'][-30:],ax=ax2)
plt.show()

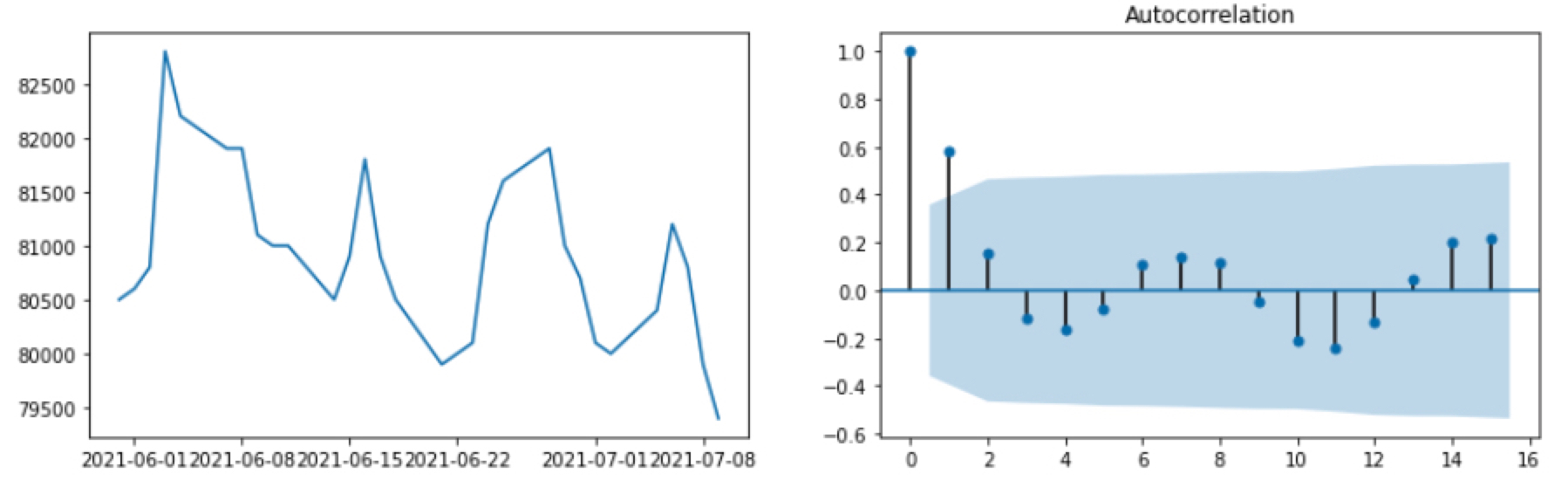
진짜로! lag=1만 허용 범위 밖이고, 나머지 lag에서는 허용 범위 안인 것 아니겠어요?
ADF 검정 결과를 보면 p-value가 0.864로 나와서 진짜 정상성을 띠는 것은 아니긴 합니다. 아마도 ACF를 보면 물결 모양처럼 나와서 그렇지 않을까 생각이 드네요.
아무튼! ACF가 빽빽하게 감소하는 모습이었으면…하는 바람이었습니다. (우상향 가즈아-!)

정상성: 통계적 시계열 분석에 필요한 가정

정상성의 정의

정상성이 중요한 이유

정상성을 만족시키기 위한 두 가지 방법

차분 (Differencing)

2차 차분

계절성 차분

로그 변환

로그 변환 + 차분 (로그 차분)

정상성 검증을 위한 두 가지 방법

그래프로 정상성 파악하기

가설 검정으로 정상성 파악하기

실전! 삼성 전자 주가 정상성을 띠도록 만들기!

여담

References