NDC 후기: 추천알고리즘 Offline A/B 테스트 (feat. PAIGE 프로야구 서비스)

Posted on 2021-12-16 Edited on 2023-05-20 In review

이 글은 NDC (Nexon Developers Conference) 홈페이지에서 YouTube 영상을 보고 관심 있던 주제인 A/B 테스트를 현업에서 어떻게 사용하는지에 대해 정리한 글입니다.

이 글은 NDC (Nexon Developers Conference) 홈페이지에서 YouTube 영상을 보고 관심 있던 주제인 A/B 테스트를 현업에서 어떻게 사용하는지에 대해 정리한 글입니다.
다음 방침에 따라 권리자명과 홈페이지를 출처로 밝힘을 알립니다.

NDC 저작권 방침: 저작물을 개인 블로그, 페이스북 등 SNS에 게재하길 원하시는 경우에는 반드시 권리자명 및 본 홈페이지를 출처로 명시하여야 하고, 해당 저작물을 변형시키지 않는 전제 하에서 게재하실 수 있습니다.

강연: 추천알고리즘 offline AB 테스트 (feat. PAIGE 프로야구 서비스)
강연자: NC 소프트 Knowledge AI Lab Curation 팀 정예원님
링크: NDC 2021 발표

오프라인 A/B 테스트의 개념

A/B 테스트는 많은 분들이 아시다시피 A와 B 알고리즘의 성능을 비교 평가하는 것을 의미합니다.
위 강연에서는 특히 하나의 서비스에 여러 개의 추천 컨셉 및 알고리즘을 적용하면서 어떤 추천 알고리즘이 가장 좋은지 알아내는 데에 A/B 테스트를 적용하였습니다.

음악 서비스를 예로 들면

인기 순
사용자가 좋아하는 가수의 음악
사용자가 좋아하는 장르의 음악
오늘 날씨에 듣기 좋은 음악

과 같이 여러 추천 방식이 있을텐데, 1 ~ 4 중 어떤 알고리즘의 성능이 가장 우수한지를 비교 평가할 수 있는 것입니다.

그렇다면 음악을 추천할 때 어떤 방식으로 추천하는 것이 사용자의 리텐션을 높일 수 있을까요?
(개인적으로는 2번 방식을 선호합니다 ㅎㅎ)
이렇게 서비스의 만족도를 높이기 위해선 어떤 알고리즘의 성능이 우수한지 비교 평가하는 것이 중요할 것입니다.

그리하여 A/B 테스트를 진행할텐데요. A/B 테스트에는 크게 두 가지 종류가 있습니다.

온라인 A/B 테스트: 실제 서비스에 A와 B 알고리즘을 모두 적용해서 성능을 비교 평가하는 것
오프라인 A/B 테스트: 과거 A 알고리즘이 실제 서비스에 적용되었던 히스토리 데이터를 이용하여 B 모델의 실제 성능을 추론해 보는 것

저희가 주로 듣게 되는 A/B 테스트는 온라인 A/B 테스트에 해당합니다. 누가봐도 온라인 A/B 테스트가 통제된 실험환경에서 랜덤하게 유저를 뽑아서 그 반응을 보는 것이기 때문에 가장 정확하고 비교하기 좋겠지만
, 현실에서는 온라인 A/B 테스트를 하지 못하는 경우도 많습니다. 왜냐하면 온라인 A/B 테스트를 하려면 충분한 데이터가 수집되기까지 많은 시간이 소요되고 리스크가 크기 때문에 비용이 높을 수 있습니다.

따라서, 대안으로 오프라인 A/B 테스트를 사용할 수 있습니다.
특히 테스트하고 싶은 알고리즘이 2개가 아니라 10개 이상이라면 모두 A/B 테스트를 하는 것은 불가능할텐데요.
이럴 경우 오프라인 A/B 테스트를 통해 우수한 알고리즘을 몇 개 골라내고 이를 온라인 A/B 테스트로 더 정확하게 볼 수 있다고 합니다.

그러나 오프라인 A/B 테스트는 실험 환경이 아니기 때문에 실제 추천 알고리즘의 성능과 다른 결론을 낼 수도 있습니다.

오프라인 A/B테스트, 왜 실제와 결과가 다를까?

이에 정예원님께선 쉬운 예제로 그 이유를 설명하셨습니다.

음악 서비스를 예로 들어보면 다음과 같습니다.
타겟이 되는 사용자는 인디밴드를 좋아하는 20대 여성이고, 당시 맑은 봄이라고 가정을 해보겠습니다.

적용된 A 알고리즘은 사용자가 좋아하는 인디밴드 장르의 음악을 추천하는 방식이고, B 알고리즘은 맑은 봄 날씨에 어울리는 음악을 추천하는 방식입니다.

이 때 A 알고리즘은 이미 적용된 알고리즘이기 때문에 사용자의 반응을 알 수 있지만, 테스트해보고자 하는 B 알고리즘은 서비스에 적용된 적이 없기 때문에 사용자의 반응을 알기 어렵습니다.
과거 데이터를 이용해서 B 알고리즘의 반응을 확인한다 하더라도, 이 사용자가 A 알고리즘에 의해 추천되었던 노래 "여행"에 대해서만 그 반응을 알 수 있습니다.

이렇듯 과거 데이터는 A 알고리즘과 그로부터 생성된 사용자의 반응에 편향되어 있습니다.
즉, 이미 적용된 알고리즘 A를 통해 추천된 콘텐츠 (= 여행)에 대해서만 반응을 평가할 수 있고 테스트 알고리즘이 새롭게 제시할 "햇살이 아파"와 “나만, 봄” 콘텐츠에 대한 사용자의 선호도를 평가하기 어렵습니다.

이러한 한계를 극복하기 위한 방법으로 Counterfactual thinking 접근 방법이 주목을 받고 있습니다.
항상 인과추론에서 나오는 Counterfactual, 이번 기회에 잘 알아봅시다.

Counterfactual Thinking을 쉽게 풀면 다음과 같습니다.

“만약 뫄뫄를 했다면 (조건), 뭐뭐 했을 텐데 (결과)”

이렇게 "뫄뫄"에 해당하는 부분은 실제로 일어나지 않았기 때문에 Counter (반) Factual (사실)적인 부분에 해당합니다.
위 문제에 대응시킨다면 만약 "어떻게 지내"라는 음악이 A 알고리즘이 아닌 B 알고리즘에 의해 첫번째로 추천되었다면 20%의 확률로 추천되었을텐데로 생각해볼 수 있는거죠.

여기서 B 알고리즘의 추천 확률 개념을 이용해서 사용자의 반응을 re-weighting 하는 방법으로 위에서 말씀드렸던 한계를 극복할 수 있다고 합니다.
이 오프라인 A/B 테스트는 야후, 마이크로소프트, 넷플릭스 등 많은 기업들이 시도하고 있는 방법이고 2018년을 시작으로 추천 시스템 학회에서 잘 나오는 주제라고 합니다.

자, 여기까지 이해가 되셨나요? 저는 이때까진 어떻게 20%확률로 추천된다는지 안다는 건지 잘 이해가 되지 않았습니다.
다음 주제에서 어떻게 "re-weighting"을 하는지 아실 수 있습니다!

오프라인 A/B 테스트의 근간이 되는 Importance Weight

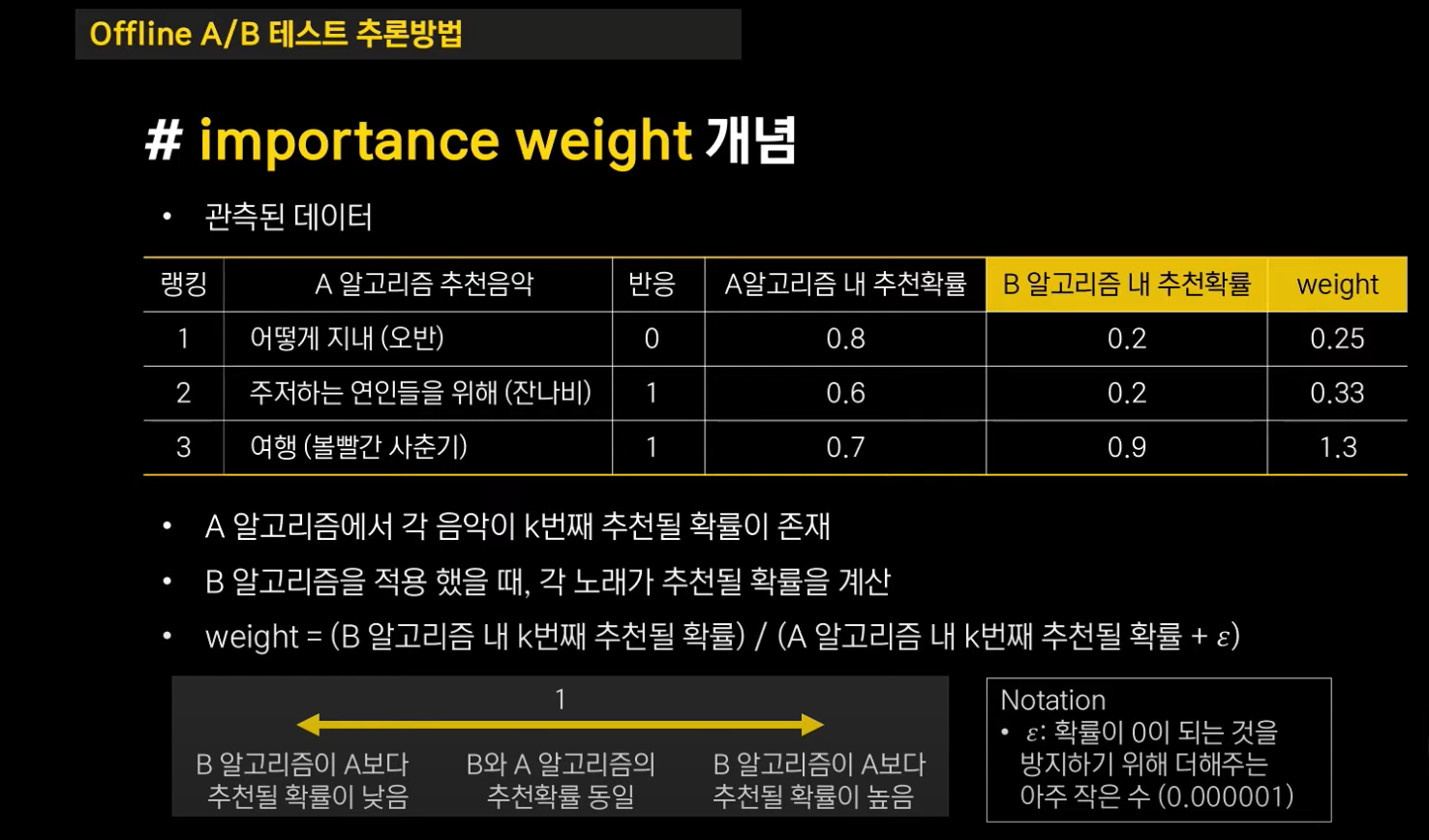
먼저 관측된 데이터는 A 알고리즘에 의해 추천된 음악입니다. 예를 들어 위 세 음악을 추천했고 두 개의 음악에 대해 반응을 했다면 A 알고리즘의 반응률은 2/3 즉 66.6%가 됩니다.
또한 A 알고리즘 고정된 알고리즘이 아니라면^{실제 강연에서는 A 알고리즘이 stochastic 알고리즘이라면 적용된다고 말씀을 하셨는데, 이를 Ranking이 매번 고정되지 않고 확률적으로 결정된다고 이해하였습니다.}
각 노래가 $k$ 번째 순서로 추천될 확률이 존재합니다.
만약 "어떻게 지내"가 A 알고리즘에서 첫번째로 추천되는 확률이 80%, "주저하는 연인들을 위해"가 A 알고리즘에서 두 번째로 추천되는 확률이 60%, "여행"의 경우 70%의 확률을 가진다고 가정합시다.

여기서 A 알고리즘 내 추천 확률에 B 알고리즘 내 추천 확률을 적용하는 것이 핵심입니다.
B 알고리즘을 실제 적용하진 않았지만 과거의 추천 상황을 재현하고 A 대신 B 알고리즘을 적용했을 때 각 노래가 $k$ 번째 적용될 확률을 계산할 수 있습니다.
이를 몬테칼로 시뮬레이션 (Monte Carlo Simulation) 방법이라 합니다.

예를 들어 1,000번의 추천 리스트를 생성한 후에 B 알고리즘이 "어떻게 지내"라는 노래를 첫 번째로 200번 추천되었다면 확률은 200 / 1,000 = 20%가 되는 것입니다.
이렇게 몬테칼로 시뮬레이션을 통해서 B 알고리즘 내 $k$ 번째 추천될 확률을 각각 20%, 20%, 90% 라고 가정합시다.

그렇게 A와 B 알고리즘에 대해 각 노래가 $k$ 번째 추천될 확률을 구하고 나면 노래마다 가중치를 계산할 수 있습니다.

가중치 = (B 알고리즘 내 k번째 추천될 확률) / (A 알고리즘 내 k번째 추천될 확률 + $\epsilon$ )

이렇게 가중치를 계산하고 나면 1을 기준으로 다음과 같이 생각할 수 있습니다.

가중치 = 1: B와 A 알고리즘의 추천확률이 동일
가중치 > 1: B 알고리즘이 A 알고리즘보다 추천될 확률이 높음
가중치 < 1: B 알고리즘이 A 알고리즘보다 추천될 확률이 낮음

즉 예시에서 보면 "어떻게 지내"나 "주저하는 연인들을 위해"는 A보다 B 알고리즘에서 추천될 확률이 낮으므로 가중치가 1보다 작고, "여행"의 ,노래는 A보다 B에서의 추천 확률이 높기 때문에 가중치가 1보다 높습니다.

이 가중치를 계산하고 나선!!! B 알고리즘의 추정 반응률을 계산할 수 있습니다. 바로 아래와 같이 말이죠.

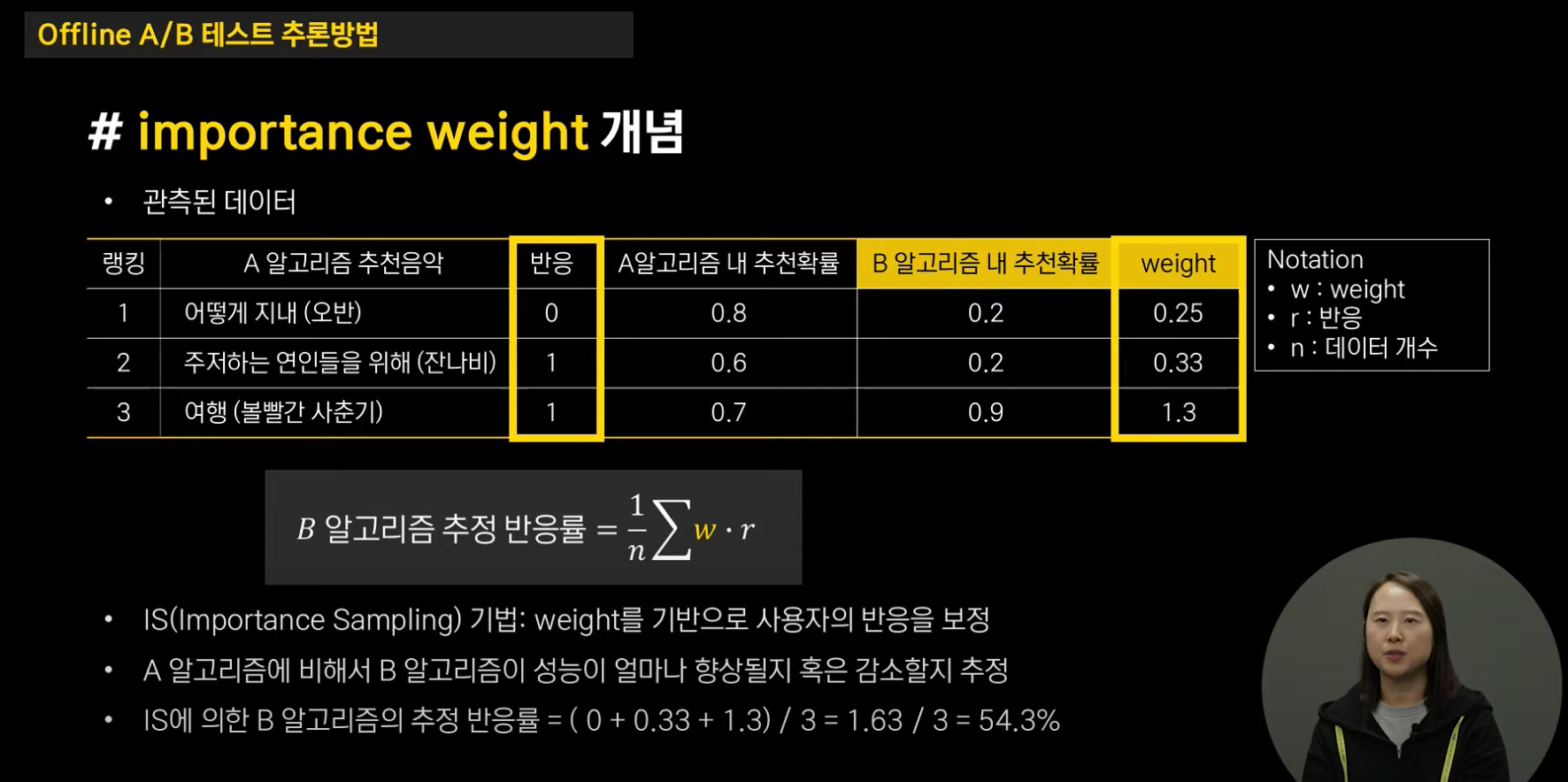
반응률 식을 보면 A 알고리즘에서 반응했는지의 여부 (r = {0, 1})과 가중치 (w)를 곱해준 것에 대해 평균으로 나눠주고 있습니다.
이 식을 해석해보자면

"주저하는 연인들을 위해"의 경우, A 알고리즘에서 반응을 했을지더라도 가중치가 낮은 (=B 알고리즘의 추천 확률이 낮은) 노래는 반응을 할 확률이 0.33으로 낮아지고
"여행"의 경우, A알고리즘에서 반응을 했고 B 알고리즘에서도 추천확률이 높기 때문에 1.3이라는 높은 값을 가집니다.

이렇게 가중치를 기반으로 사용자의 반응을 보정하는 방법이 주표본(표집) 기법 (Importance Sampling) 기법입니다.
실제로 계산해보면 B 알고리즘의 추정 반응률은 (0+0.33+1.3) /3 = 1.63 / 3 = **54.3%**가 나오게 됩니다.

예전에 Importance Sampling에 대해 배웠던 기억이 있어 강의 노트를 찾아보았습니다.
원래 Importance sampling 방법은 적분을 하기 어려운 함수가 있을 때, 몬테칼로 시뮬레이션을 통해서 표본을 추출하여 적분을 근사하는 방법입니다.

예를 들어 $g(x)$ 라는 함수가 굉장히 복잡한데 $f(x)$ 로 나눠주었을 때 함수 꼴이 확 쉬워진다면 이 방법을 시도해볼 수 있습니다.

I =\int g(x) dx = \int \frac{g(x)}{f(x)} f(x) dx = E \left(\frac{g(x)}{f(x)}\right)

최종적으로, 위에서 기댓값인 $E \left(\frac{g(x)}{f(x)}\right)$ 에 대해서 $x_1,\ldots, x_n$ 을 따르는 난수를 생성해서 이렇게 적분값을 근사할 수 있습니다. (마치 모평균을 표본 평균으로 대체하는 그 원리…!)

I \approx \frac{1}{n} \sum_{i=1}^n \frac{g(x_i)}{f(x_i)}

이를 위 상황에 적용해보면 아래와 같을 것 같습니다. (!뇌피셜이라 논리에 구멍이 있을 수 있음 주의!)

$g(x)$ 에 해당하는 것은 B 알고리즘을 적용했을 때 $k$ 번째 추천될 확률, $f(x)$ 에 해당하는 것은 A 알고리즘을 적용했을 때 $k$ 번째 추천될 확률에 해당합니다.
이 확률을 추정하기 위해 1,000번 동안 알고리즘을 돌려서 B 알고리즘과 A 알고리즘 내에서 "어떻게 지내"라는 노래가 첫 번째로 추천될 확률을 각 구하면 $g(x_i) / f(x_i)$ 즉 앞서 가중치가 계산이 됩니다.
이렇게 가중치와 반응을 곱해주면 기댓값을 구할 수 있지 않을까? 그래서 Importance sampling이라 하지 않을까 생각이 들었습니다.

Importance Sampling의 치명적인 단점

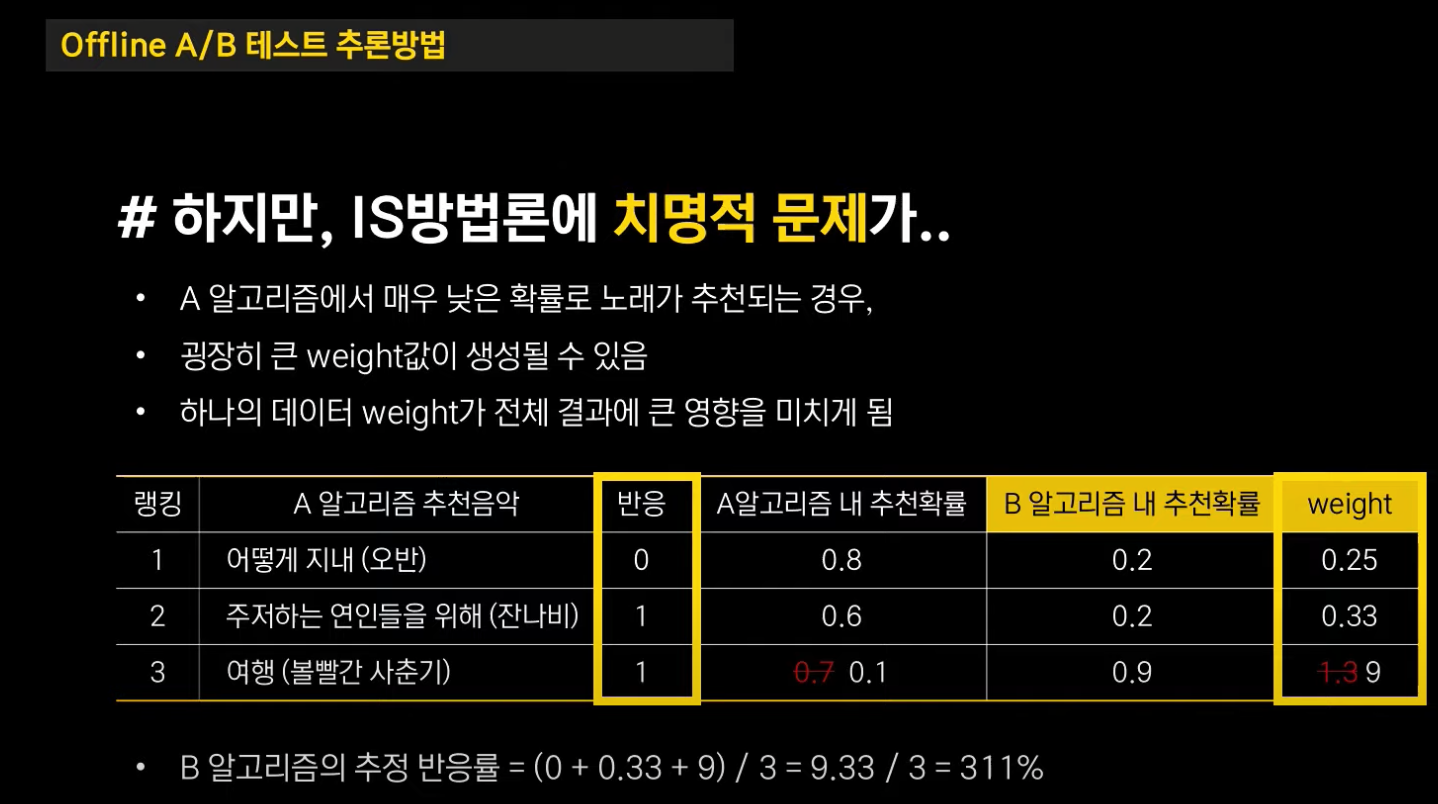
그러나 Importance Sampling은 치명적인 단점을 가지고 있습니다. 만약 A 알고리즘에서 매우 낮은 확률로 노래가 추천되는 경우, 굉장히 큰 가중치 값이 생성될 수 있습니다. 이 경우 하나의 데이터 가중치가 전체 결과에 큰 영향을 미치게 됩니다.

위 예시에서 만약 "여행"의 A 알고리즘 내 추천 확률이 0.1이라면, 가중치가 비정상적으로 높게 9로 계산이 됩니다.
이 때 그대로 B 알고리즘의 추정 반응률을 계산하게 되면 311%라는 비정상적인 수치를 갖게 됩니다.

CIS (Capping Importance Sampling), 가중치를 제한하자!

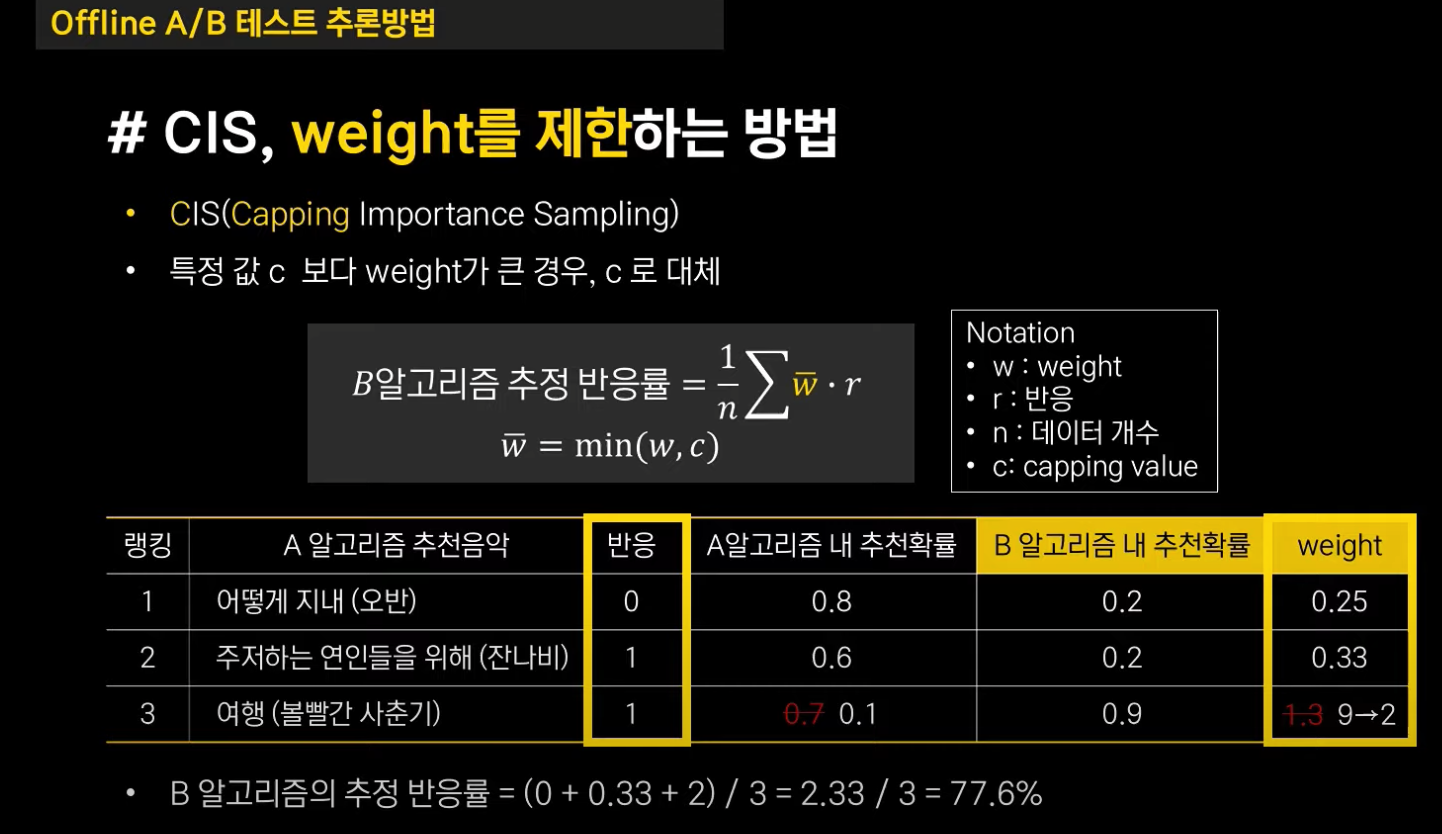
위 문제를 해결하기 위한 방법은 가중치를 조정하는 것입니다. 가중치가 비정상적으로 높다면, 최댓값을 capping value인 $c$ 로 제한하면 됩니다.
위 예제에선 비정상적인 가중치 9 대신에 capping value를 2로 임의로 두고 B 알고리즘의 추정 반응률을 계산했더니 77%로 가중치가 보정되었습니다.

이 외에도 NCIS (Normalized Capping Importance Sampling) 방법도 있다 합니다. 이 방법은 CIS 값을 정규화해서 예측 에러를 최소화시킨 추정값이라 합니다.

실제 사례: KBO 프로 야구 AI 어플, PAIGE

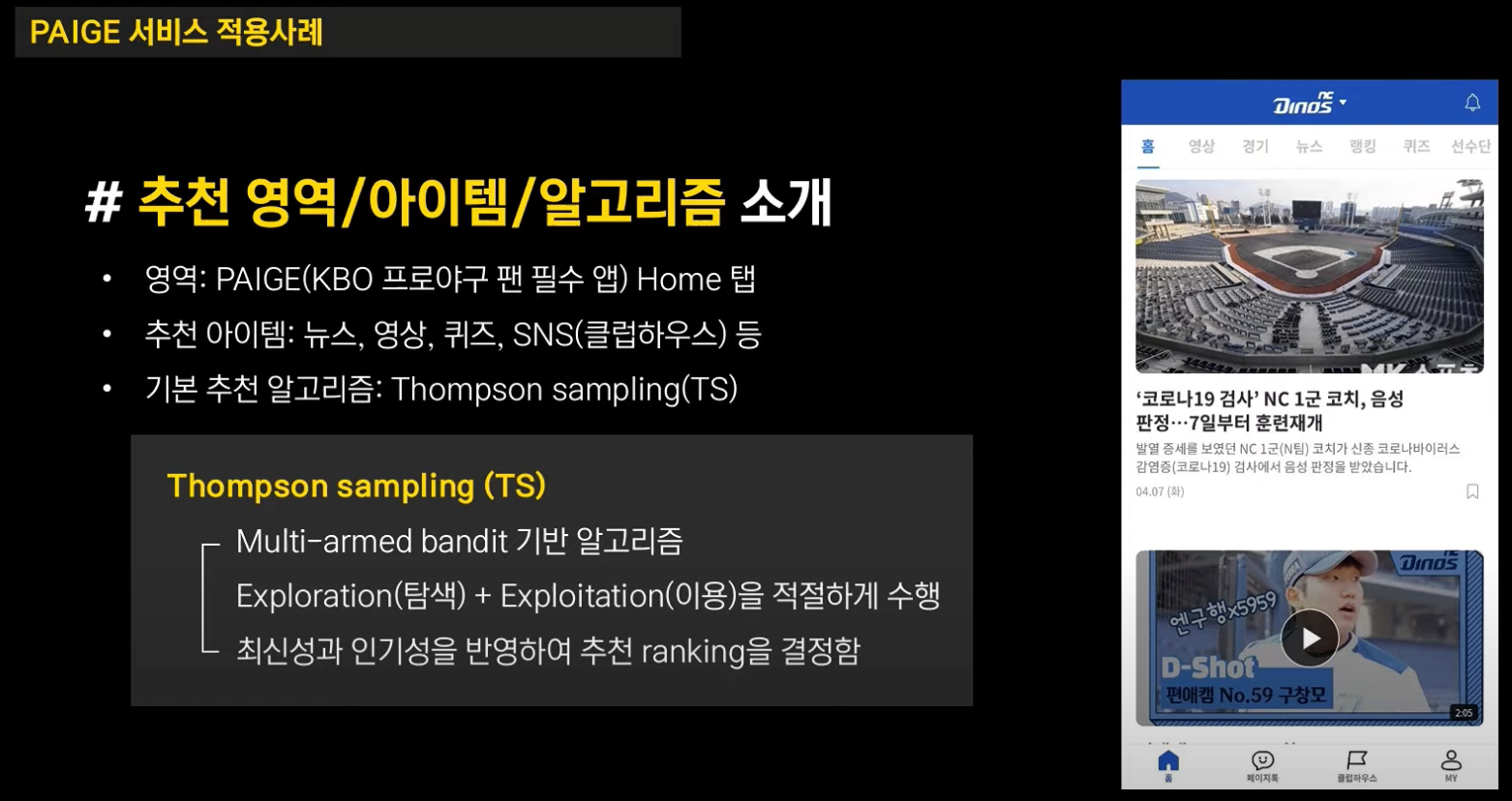
위 그림처럼 PAIGE는 KBO 프로 야구의 정보를 담은 어플로, 뉴스, 영상, 퀴즈, SNS 등을 추천하고 있다고 합니다.
여기서, 기존에 적용되던 A 알고리즘은 톰슨 샘플링으로 구현된 야구 뉴스, 피드 페이지고
테스트하고자 하는 B 알고리즘은 톰슨 샘플링에 선호구단을 반영해 추천하는 방식입니다.

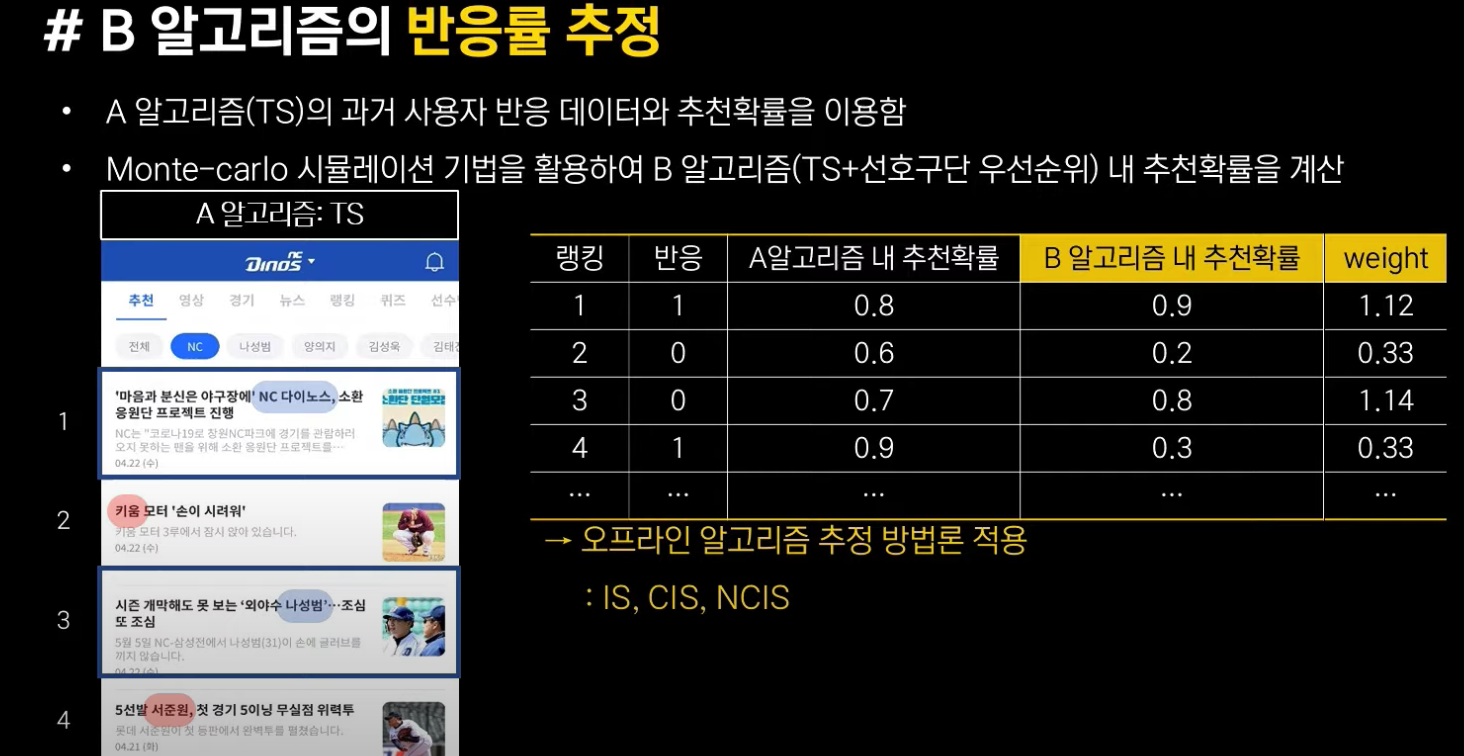
이렇게 앞에서 설명드린대로

A 알고리즘의 과거 데이터를 이용해 반응 여부와 추천 확률을 계산하고,
B 알고리즘 내 추천확률을 몬테칼로 시뮬레이션을 통해 계산합니다.
이를 통해 가중치를 계산합니다.

그림을 자세히 보시면 첫 번째, 세 번째 피드는 선호 구단인 "NC 다이노스"에 대한 피드이므로 선호구단 순위를 알고리즘에 녹인 B 알고리즘 내에서 추천 확률이 0.9, 0.8로 높지만, 두 번째, 네 번째 피드는 다른 구단에 대한 피드이므로 추천 확률이 각각 0.2, 0.3으로 낮습니다. 이에 따라 가중치도 첫 번째와 세 번째는 1보다 크게, 두 번째와 네 번째 피드는 1보다 낮게 계산됩니다.

오프라인 A/B 테스트의 검증 결과를 요약하면 다음과 같습니다.

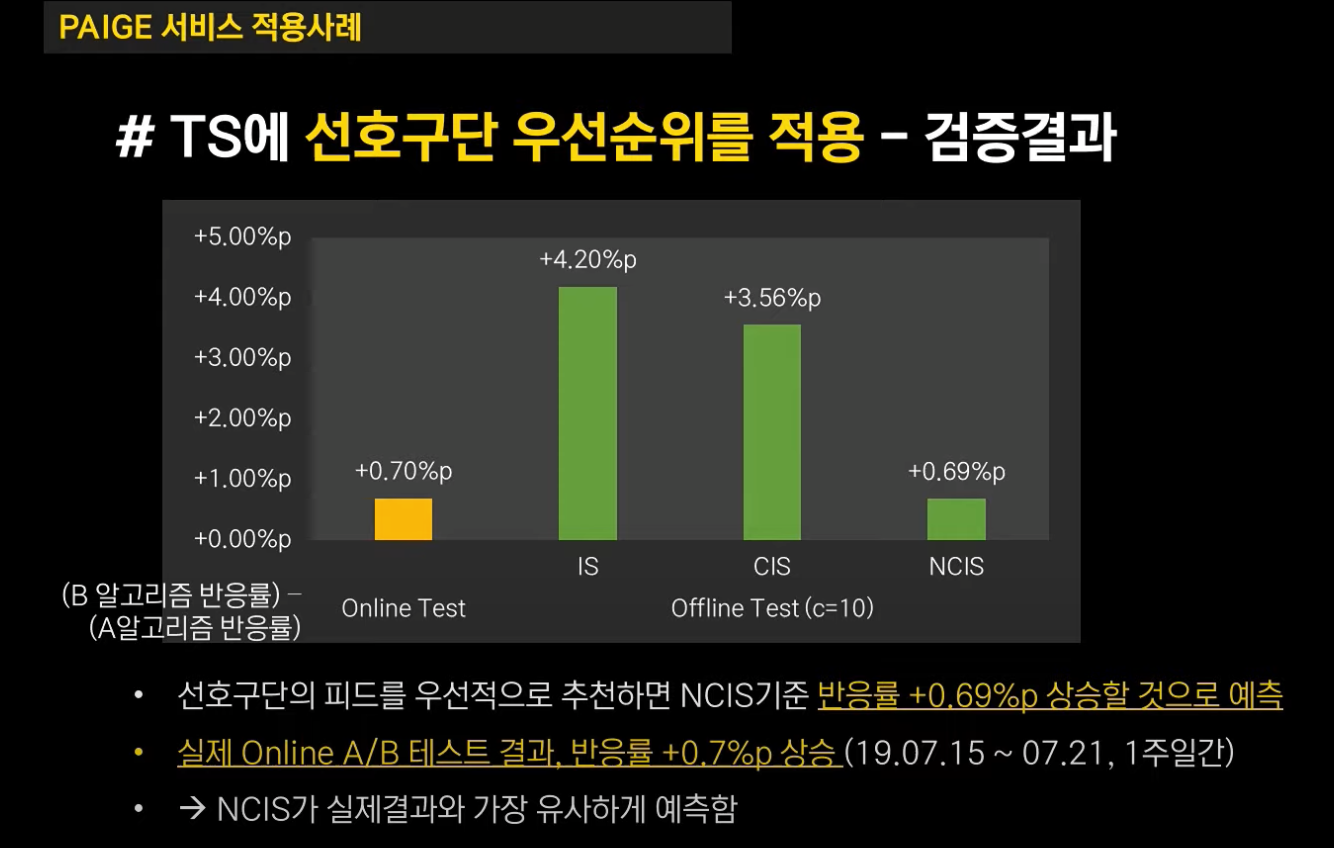
톰슨 샘플링의 기존 알고리즘에 선호 구단의 피드를 우선적으로 알고리즘을 더하면 NCIS 기준 반응률이 0.69%p 상승할 것으로 예측했습니다.
또한 실제 A/B 테스트 결과에도 반응률이 0.7%p 상승한 결과를 나타내어 오프라인 A/B 테스트와 온라인 A/B 테스트 간 결과가 유사함을 검증했다 합니다.

글을 마치며

이 강연을 들으면서 느낀 점은 크게 두 가지였습니다.

첫 번째로, 오프라인 A/B 테스트라는 것을 처음 접했는데 실제로 회사에서 적용해보면 재밌겠다 생각이 들었습니다. 그렇게 weight를 계산하는 것이 어렵지는 않으니까 말이죠.
그러나 여기서 문제를 단순화해서 쉬워보이지 뭔가 실제로 했을 때 여러 난관이 있을 것 같습니다.
특히 추천 대상인 "음악"이 10만 개라면 ranking에 따른 정렬을 어떻게 하는지 궁금했습니다.
"어떻게 지내"가 첫 번째로 추천될 확률을 구해야하는지, 혹은 10번 째로 추천될 확률을 구해야 하는지 등 ranking 1~ 10만에 대해 어떻게 정렬을 해서 계산을 하는 건가에 대한 의문점이 들었습니다.

두 번째 느낀 점은 0.7%p 가 과연 높은 수치일까…? 통계적으로 유의미한 차이일까 ? 이런 생각이 들었습니다.
통계적 유의성은 알기 어려우니 0.7%p에 대한 기대 효과를 대강 계산해보았습니다.
일별로 유저가 10,000명 어플에 접속한다 가정했을 때 0.7%p면 70명이 더 반응한 것이고 월별로 단순 계산하면 2,100명이 더 반응한 꼴이 됩니다.
만약에 이 어플이 구독형 어플이고 월별 구독료가 3,000원이라 치면 월 62만 원의 추가 수익을 얻는 것이죠!
그런데, 만약 개발 리소스가 부족하여 많은 직원들이 야근을 하고 야근 수당을 타간다면…! 절대 62만 원 가지곤 만족할만한 수치가 아니라 생각이 들었습니다.

오랜만에 NDC를 들으니 또 재밌네요 😃 주최하는 곳이 저희 회산데… 내년엔 오프라인으로 듣고 싶습니다… ㅎㅎ