인과 관계 분석 시리즈 (3): 성향 점수 매칭 (Propensity Score Matching)과 층화 (Stratification)

Posted on 2020-06-21 Edited on 2023-05-20 In statistics

이번 포스팅은 Amit Sharma, Emre Kiciman님의 gitbook을 번역하면서, Matching과 Stratification을 이용한 인과관계 추론에 대해 정리하였습니다.

이번 포스팅은 Amit Sharma, Emre Kiciman님의 gitbook[link]를 번역하면서, Matching과 Stratification을 이용한 인과관계 추론에 대해 정리하였습니다.
예시로 kaggle의 Bike Sharing Demand 데이터를 이용해 인과 관계를 분석해보았습니다.
전체 코드는 이 곳에서 확인하실 수 있습니다.

Introduction

인과 관계 추론의 목적은 처리 (Treatment) $Z$ 가 결과 (Outcome) $Y$ 에 미치는 효과를 추정하는 것입니다.

그러나 교란변수 (Confounder) $X$ 는 $Z$ 와 $Y$ 에 모두 영향을 주어 $Z$ 의 순수 효과를 추정하는 것을 방해합니다. 따라서 $Z\rightarrow Y$ 의 인과관계를 추정하기 위해서는 $X\rightarrow Z$ 의 종속 관계를 끊는 것이 중요합니다.

무작위 통제 환경 (Randomized experiments)에서는 처리를 랜덤하게 배치함으로써 교란변수 $X$ 가 처리 $Z$ 에 영향을 주지 않도록 (독립이도록) 만듭니다.

예를 들어 운동 (=처리, $Z$ )이 콜레스테롤 수치 (= 결과, $Y$ )에 어떻게, 얼마나 영향을 주는 지 관심이 있다 가정합시다. 근데 사람의 나이 (=교란변수, $X$ )에 따라서 운동의 빈도가 다를 수 있고, 콜레스테롤 수치가 변할 수 있습니다. 가령 나이가 30세인 사람은 6세인 사람보다 건강에 신경을 써서 운동을 더 많이 하고, 콜레스테롤 수치가 나이가 듦에 따라 더 높을 수 있습니다. 이를 DAG (Directed Acyclic Graph)로 나타내면 다음과 같습니다.

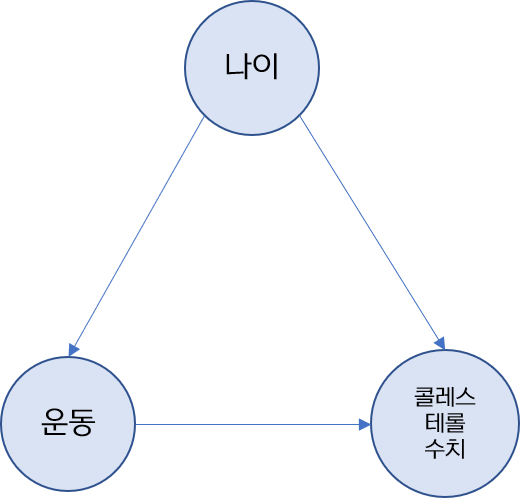
따라서, 운동 $\rightarrow$ 콜레스테롤 수치의 효과를 추정하기 위해서는 나이 $\rightarrow$ 운동의 종속관계 (dependency)를 끊어야 합니다.

무작위 통제 환경은 나이에 무관하게 운동을 무작위로 배치해서 나이와 운동이 독립이도록 합니다. 예를 들어, 실험을 하는데 여러 나이대의 피실험자들이 1주동안 0번, 3번, 5번의 빈도로 1시간 동안 러닝머신을 뛰었을 때, 콜레스테롤 수치의 변화를 보고자 한다 가정합시다. 이 때 무작위 통제 환경은 이 운동 빈도를 랜덤하게 배치해 나이와 운동 빈도가 독립이도록 합니다.

위의 예시에서 "운동"을 “자전거 타기” (Stationary Biking)라 해봅시다. 마찬가지로 운동 빈도에 따라 콜레스테롤 수치가 어떻게 변화했는 지 보고 싶어서 자전거 타기 빈도를 X축에, 콜레스테롤 수치를 Y축에 두고 산점도를 그려봤더니 상식에 어긋난 결과를 얻게 됩니다.

상식 상 "운동을 많이 하면 콜레스테롤 수치가 낮아질 것"이라는 가정이 있지만, 위 그림은 운동 빈도가 많아질수록 콜레스테롤 수치도 높아지는 추세를 보입니다.

왜 그럴까요? 나이를 고려하지 않고 산점도를 그렸기 때문입니다. 아래의 그림처럼 나이를 고려하고 그림을 다시 그리게 되면, 나이 그룹 내에서는 운동 빈도가 많아질수록 콜레스테롤 수치는 낮아지는 추세를 보입니다.

이런 현상이 일어난 이유는 나이가 교란변수로써 운동빈도와 콜레스테롤 수치에 모두 영향을 미쳤기 때문입니다. 즉, 나이가 많아질수록 운동빈도와 콜레스테롤 수치 모두 높아지는 경향 때문에 운동빈도에 따른 콜레스테롤 수치 변화가 음(-)의 관계가 아니라 양(+)의 관계처럼 보였던 거지요. 이런 현상은 심슨 패러독스 (Simpson’s Paradox)의 예라고 할 수 있습니다.

따라서 다음과 같이 교란변수인 나이를 조건으로 잡아서 자전거 타기 빈도에 따른 콜레스테롤 수치의 확률을 구할 수 있습니다.

P(\text{콜레스테롤 수치}\vert do(\text{자전거 빈도})) = \sum_{\text{나이}} P(\text{콜레스테롤 수치}\vert \text{자전거 빈도,나이})P(\text{나이})

여기서의 가정은 무엇일까요?

Ignorability: 나이가 유일한 교란 변수 (자전거 빈도와 콜레스테롤 수치에 모두 영향을 주는 유일한 변수)
SUTVA (Stable Unit Treatment VAlue): 자전거 타기의 효과는 다른 친구들의 운동에 영향을 주지 않음
Common support (Overlap): 운동한 사람과 운동하지 않은 사람들은 비슷한 사람들을 cover함

이게 무슨 소리냐구요? 이 가정들에 대한 설명을 자세히 해보겠습니다.

가정1: Ignorability

랜덤화 실험 환경에서는 처리와 교란변수가 관측되거나 관측되지 않은 공변량 (covariates) 모두에 대해 독립입니다. 그러나 Conditioning 방법은 관측된 공변량 ( $X$ )에 대해서만 처리와 독립이라고 말할 수 있습니다.

따라서 Ignorability 가정은 관측된 공변량을 조건으로 했을 때 관측되지 않은 공변량이 모두 처리와 무관하다는 가정입니다.

가정2: SUTVA (Stable Unit Treatment VAlue)

SUTVA 가정은 한 개인의 처리가 다른 사람의 결과에 영향을 미치면 안됨을 의미합니다.

이를 수식으로 나타내면 다음과 같습니다.

P[Y_i \vert do(Z_i, Z_j)] = P[Y_i \vert do(Z_i)]

예를 들어 XBOX 콘솔에 대한 긍정적인 리뷰가 XBOX 콘솔 뿐 아니라 컨트롤러와 같은 XBOX 악세서리의 수요를 증가시켰다면 SUTVA 가정을 만족하지 못합니다. 왜냐하면 XBOX 콘솔에 대한 긍정적 리뷰 (한 물품의 처리)가 XBOX 콘솔의 매출 증가 (처리 효과)뿐 아니라 XBOX의 악세서리의 매출 증가 (다른 물품의 결과)를 불러일으켰기 때문입니다. 이런 효과를 Spillover 효과라 일컫습니다.

가정 3: Common Support

Common Support 가정은 처리받은 모집단과 처리받지 않은 모집단 간의 특성이 비슷해야 함을 의미합니다. 즉, 처리받은 집단과 처리받지 않은 집단의 관측된 공변량 간의 overlap이 필요함을 의미합니다.

이를 수식으로 나타내면 다음과 같습니다.

0< P[T=1 \vert X=x] < 1

이 세 가정이 만족한다고 가정하고, Conditioning 방법은 처리와 결과에 관련있는 변수 (공변량)들을 최대한 고려해 변수 간 인과관계를 따져 처리 효과를 계산합니다. 이는 Bayesian Network에서 변수 간 인과관계를 파악하는 것과 일맥상통합니다. 자세한 내용은 이전 포스팅을 참조해주시길 바랍니다.

근데 만약 우리가 통제된 실험 환경을 조성하지 못한다면 실험 환경처럼 최대한 비슷하게 만드는 수밖에 없습니다. 이런 관측 환경에서의 인과 관계 추론 중 제가 소개할 방법은 두 가지입니다.

Matching
Stratification

Matching

매칭 (Matching) 방법은 처리 집단과 비처리 집단 중 한 명씩 뽑아 비슷한 사람들을 찾는 것부터 시작합니다.
처리 집단의 $i$ 번째 데이터와 비처리 집단의 $j$ 번째 데이터 간의 거리를 재서 $\epsilon$ 보다 작으면 (즉, 거리가 가까운 사람들끼리) 매칭이 됩니다.

\begin{aligned} Distance(X_i, X_j) &<\epsilon\\ Distance(X_i, X_j) &= \sqrt{(\vec{x}_i-\vec{x}_j)^\top S^{-1}(\vec{x}_i-\vec{x}_j)} \end{aligned}

이렇게 짝지은 쌍들은 서로 **Counterfacutal (가상적 대응치)**가 되어 이들의 콜레스테롤 수치의 차이를 각각 구하고, 평균을 취하면 인과 관계를 측정하는 척도 중 하나인 **Average Treatment Effect on the Treated (ATT)**를 구할 수 있게 됩니다.

매칭에도 여러 종류가 있는데 가장 기본적인 매칭의 거리 척도는 Mahalanobis 거리입니다. Mahalanobis 거리는 공분산 행렬로 각 차원을 정규화해 단위 거리를 계산합니다. 식은 다음과 같습니다.

\text{Mahalanobis}\left( \overrightarrow{x}_i, \overrightarrow{x}_j \right) = \sqrt{(\overrightarrow{x}_i - \overrightarrow{x}_j)^\top S^{-1} (\overrightarrow{x}_i - \overrightarrow{x}_j)}

여기서 $x_i$ 는 $i$ 번째 데이터의 행렬, $S$ 는 공분산 행렬 (covariance matrix)입니다.

Matching by Propensity Score (성향 점수를 통한 매칭)

성향 점수 (Propensity Score)는 교란변수를 조건으로 했을 때 처리받을 확률을 추정합니다. 즉,

\widehat{e}(X) = P[Z=1 \vert X]

이렇게 교란변수를 조건으로 하는 성향 점수를 이용하면 $Z\rightarrow Y$ 를 추정하는 데 교란변수 $X$ 의 영향을 배제할 수 있기 때문에 성향점수를 이용해 매칭을 합니다.

어떻게 하냐구요?

교란변수 ( $X$ )들을 피처로, 처리 여부 ( $T$ )를 결과로 두고 이를 예측하기 위한 지도학습의 머신러닝 모형을 훈련시킵니다. 로지스틱, SVM, GAM 등을 사용해 성향점수 ( $\widehat{e}(x_i) = P[Z=1\vert x_i]$ )를 예측합니다.
성향 점수 간 거리를 계산해 처리그룹과 비처리 그룹 한 명씩 가장 가까운 짝을 찾습니다.
이들의 결과의 차를 계산 하고 평균을 취해 ATT^{Average Treatment effect on the Treated}를 계산합니다.

이에 대한 pseudo python 코드는 다음과 같습니다.

# 성향점수 머신러닝 모형 (여기선 선형 모형) 
psmodel = lineara_model.LinearRegression()
psmodel.fit(covariates, treatment_status)
data["ps"] = psmodel.predict(covariates) # propensity score

# 처리 그룹의 최근접 이웃을 비처리 그룹에서 찾기
controlMatcher = NearestNeighbors().fit(untreataed["ps"])
distances,matchIndex = controlMatch.kneighbors(treated["ps"])

# 매칭된 쌍끼리 결과값의 차이를 구해서 att에 더해주고
for i in range(numtreatedunits):
   treated_outcome = treated.iloc[i][outcome_name].item()
   untreated_outcome = untreated.iloc[mathIndex[i]][outcome_name].item()
   att += treated_outcome - untreated_outcome

# att를 처리인원수로 나눠주기
att /= numtreatedunits

Stratification^층화

매칭이 1:1로 비슷한 데이터를 찾는 것이었다면, 층화는 many:many로 집단 단위에서 비슷한 데이터를 찾아 집단 별로 차이를 계산하는 방법입니다.

Stratification by Propensity Score

매칭과 마찬가지로 성향점수를 바탕으로 매칭 대신 층화를 하여 ATT를 계산합니다.

ATT = \sum_{s\in{\text{strata}}} \frac{1}{N_{s,T=1}} \left(\overline{Y}_{s,T=1} - \overline{Y}_{s,T=0}\right)

여기서

$\overline{Y}_{s,T}$ 는 처리 여부 $T$ 와 층 (strata) $s$ 에 따른 평균 결과치
$N_{s,T=1}$ 는 $s$ 번째 층의 처리받은 사람 수

를 의미합니다. 이에 대한 pseudo 코드는 다음과 같습니다.

# 성향점수에 따라서 층에 대한 열을 만들어주기
data['strata'] = ((data['ps'].rank(ascending=True) / numrows) * numStrata).round(0)
data["T_y"] = data["T"] * data["outcome"] #처리 집단의 결과값
data["Tbar"] = 1-data["treated"] # 비처리집단
data["Tbar_y"] =  data["Tbar"] * data["outcome"] #비처리집단의 결과값
stratified = data.groupby("strata")

outcomes = stratified.agg({"T":["sum"], "Tbar":["sum"], "T_y":["sum"], "Tbar_y":["sum"]})

# 층 효과 계산
outcomes["T_y_mean"] = outcomes["T_y_sum"] / outcomes["T_sum"]
outcomes["Tbar_y_mean"] = outcomes["Tbar_y_sum"] / outcomes["Tbar_sum"]
outcomes["effect"] = outcomes["T_y_mean"] - outcomes["Tbar_y_mean"]

# 층 효과 가중합
att = (outcomes["effect"]*outcomes["T"].sum() / totaltreatmentpopulation)

그럼 층을 몇 개를 구성해야 할까요?

데이터에 따라 다릅니다. 전통적으로 100개 미만의 데이터에서는 5개의 층을 고르고, 10,000개 ~ 100만 개 정도의 데이터라면 100~1000개 정도의 층을 구합니다.

Example : Kaggle 자전거 수요 데이터

인과 관계를 설명하기 위해 가져온 예시 데이터는 kaggle의 Bike Sharing Demand입니다. 간단한 EDA를 통해 처리와 교란변수를 결정하고 이를 바탕으로 Python의 doWhy 패키지를 이용해 인과관계를 추정해보도록 하겠습니다!

%pip install dowhy
from dowhy import CausalModel
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = "nanumgothic"
bike = pd.read_csv("train.csv")
print(bike.shape)

데이터 설명

bike의 행은 10,886개, 열은 총 12개로 변수에 대한 설명은 다음과 같습니다.

datetime: 날짜, YYYY-MM-DD HH:MM;SS형식
season: 계절 (1 = 봄, 2 = 여름, 3 = 가을, 4 = 겨울)
holiday: 공휴일 여부 (0 = No, 1 = Yes)
workingday: 평일 여부 (0 = 주말 + 공휴일, 1 = 평일)
weather: 날씨 (1 = 맑음, 약간의 구름, 2 = 안개, 흐린 날씨, 3 = 가벼운 눈, 비, 4 = 강한 눈, 비)
temp: 온도 (섭씨)
atemp: 체감 온도 (섭씨)
humidity: 습도
windspeed: 풍속
casual: 미등록 회원의 대여수
registered: 등록 회원의 대여수
count: 총 대여수 (causal + registered)

1차 전처리

1. 날짜 전처리

datetime 열을 연도 (year), 월 (month), 일 (day), 시간 (hour), 요일 (dayofweek)로 나누어 저장했습니다.
dayofweek의 경우 0 = 월, 1 = 화, …, 6 = 일의 값을 가집니다.

2. 계절, 날씨 전처리

원래 있는 계절 변수인 season이 1~3월이면 봄, 4~6월이면 여름, 7~9월이면 가을,10~12월이면 겨울인 식이라 이대로 쓰지 않고 3~5월이면 봄, 6~8월이면 여름,9~11월이면 가을, 12~2월이면 겨울이도록 바꿨습니다.

또한 날씨 변수 weather의 값이 1~4로 되어있는 걸 각각 clear, cloudy, light_rainy, heavy_rainy로 바꿨습니다.

3. 원 핫 인코딩

추후 분석을 위해 계절과 날씨에 대해 각 4개의 더미변수로 만들었습니다.

1
2
3

season_dummies = pd.get_dummies(bike['season']).rename({1:"spring",2:"summer",3:"autumn",4:"winter"},axis="columns")
weather_dummies= pd.get_dummies(bike['weather']).rename({1:"clear",2:"cloudy",3:"light_rainy",4:"heavy_rainy"},axis="columns")
bike = pd.concat([bike,season_dummies,weather_dummies],axis=1)

4. 변수 삭제

등록 여부에 따라 분석을 하진 않을 거라서 casual, registered 변수를 제외하고, 기존의 season과 weather 변수도 삭제했습니다.

1~4의 과정을 거친 파이썬 코드는 다음과 같습니다.

펼쳐보기

def month_to_season(x):
    if x in [3,4,5]:
        y = "spring"
    elif x in [6,7,8]:
        y = "summer"
    elif x in [9,10,11]:
        y = "autumn"
    else:
        y = "winter"
    return (y)

def weather(x):
    if   x==1:
        y = "clear"
    elif x==2:
        y = "cloudy"
    elif x==3:
        y = "light_rainy"
    else:
        y = "heavy_rainy"
    return (y)
# 1. 날짜 전처리
bike['datetime'] = pd.to_datetime(bike['datetime'])
bike['year']  = bike['datetime'].apply(lambda x: x.year)
bike['month'] = bike['datetime'].apply(lambda x: x.month)
bike['day']   = bike['datetime'].apply(lambda x: x.day)
bike['hour']  = bike['datetime'].apply(lambda x: x.hour)         # 시간대
bike['dayofweek'] = bike['datetime'].apply(lambda x:x.weekday()) # 요일

# 2. 계절 & 날씨 전처리
bike['season'] = bike["month"].apply(lambda x: month_to_season(x))
bike['weather'] = bike["weather"].apply(lambda x: weather(x))

# 4. 원핫 인코딩 생성
season_dummies = pd.get_dummies(bike['season'])
weather_dummies= pd.get_dummies(bike['weather'])
bike = pd.concat([bike,season_dummies,weather_dummies],axis=1)

# 5. 변수 삭제
bike = bike.drop(["casual","registered"],axis=1)

EDA

연도, 월, 일, 시간대 별 대여량

연도는 2011년보다 2012년 대여량이 더 높습니다.
월 별로 봤을 때는 1월, 2월은 대여량이 낮고 6월이 가장 대여량이 많습니다. 7~9월도 비슷하게 높은 대여량 수준에 있습니다.
일 별은 그런 큰 차이를 보이고 있진 않습니다.
시간 별 대여량은 큰 차이를 보입니다. 출퇴근 시간대인 8시나 17시는 대여량이 가장 많고, 그 사이 시간인 9~16시는 대여량이 낮은 수준에 있습니다. 또한 17시 이후부터 새벽 4시까지는 대여량이 지속적으로 감소하는 모습을 보입니다.

계절, 날씨, 근무일 여부, 휴일 여부에 따른 대여량

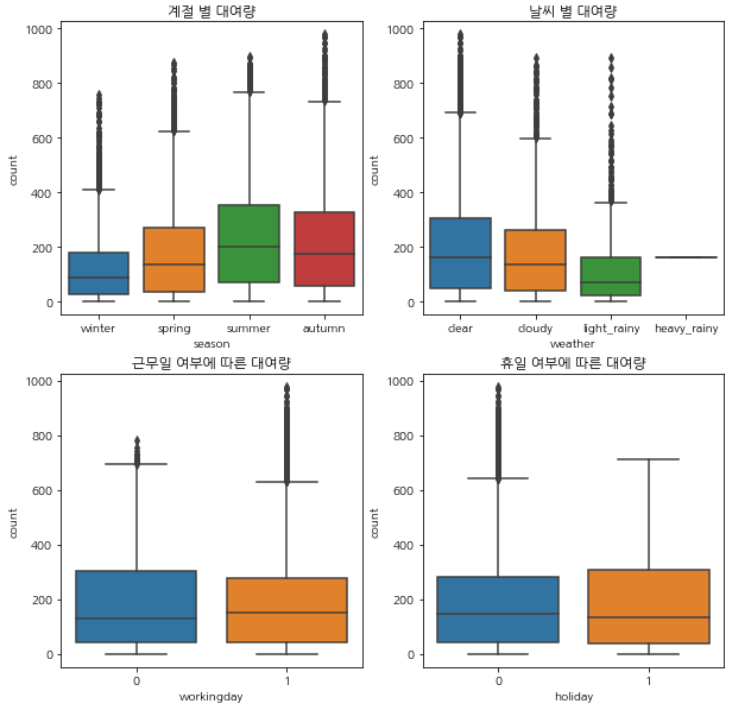
계절은 겨울에 가장 대여량이 낮고, 여름에 가장 높습니다.
날씨는 특히 비가 올 때 낮고, heavy_rainy일 때의 값은 한 값만 존재합니다.
근무일이나 휴일 여부에 따른 대여량은 크게 차이나지 않습니다.

결과적으로 자전거 대여량에 영향을 주는 주요 변수는

날씨 중 heavy_rainy나 light_rainy
계절 중 겨울
시간대
연도

입니다.
여기서 저는 날씨가 가장 크게 자전거 대여량에 영향을 미친다 파악하고 처리로 선정했습니다.

2차 전처리

2차 전처리는 날씨가 heavy_rainy거나 light_rainy이면 is_rainy = 1의 값을 갖도록 처리했습니다.

1	bike["is_rainy"]=bike["weather"].apply(lambda x: True if x == "heavy_rainy" or x== "light_rainy" else False)

주의해야할 점은 Python의 dowhy패키지에서 처리가 binary형이라면 0, 1의 int형 대신 True와 False값을 갖는 boolean형을 써줘야 한다는 점입니다.

Causal Inference using doWhy Package in Python

이제 처리 (is_rainy)와 2개의 방법 (Matching, Stratification by Propensity Score)에 따라 인과관계를 추정하기 위해 Microsoft사에서 개발한 dowhy 파이썬 패키지를 이용했습니다.
dowhy에서 인과관계를 추정하는 단계는 다음과 같습니다.

인과 모형 초기화 (Initializing causal model)
인과 효과 정의 (Identifying causal effect)
인과 효과 추정 (Estimating causal effect)
추정값 반박 (Refuting the estimate)

1. 인과 모형 초기화 (Initializing causal model)

dowhy 패키지를 쓸 때 유의할 점은 모형을 초기화할 때, 처리와 결과 모두에 영향을 주는 교란 변수를 잘 선정해야한다는 점입니다. 실제로 인과관계를 추정했을 때,
상식과 반대되는 결과를 얻기도 했습니다(!?) 예를 들어 비가 오면 자전거 대여량이 줄기 마련인데, ATT^{Averate Treatment Effect on the Treated}를 추정한 결과 양수로 나왔습니다.
그 이유는 강수 여부와 자전거 대여량 모두에 영향을 주는 교란 변수에 나머지 변수들을 모두 넣었기 때문입니다. 인과 구조가 잘못되면 인과 관계 추정의 결과도 신뢰하기 어렵기 때문에
미리 변수들 간의 구조를 파악하고 모형화하는 과정이 필요합니다.

최종적으로 강수여부 (처리)와 자전거 대여량 (결과) 모두에 영향을 주는 교란 변수로 온도, 체감온도, 습도, 풍속, 계절, 연도를 고려하여 common_causes에 temp, atemp, humidity, windspeed, spring, summer, autumn, is_2012를 포함하였고,

강수여부 (처리)에 영향을 주진 않지만 자전거 대여량 (결과)에 영향을 주는 공변량으로 출퇴근 시간대 여부, 휴일 여부를 고려해 effect_modifiers에 is_rush_hour와 holiday를 포함했습니다.

rainy_effect = CausalModel(
    data=bike,
    treatment = "is_rainy",
    outcome   = "count",
    common_causes = "temp+atemp+humidity+windspeed+spring+summer+autumn+is_2012".split("+"),
    effect_modifiers = "is_rush_hour+holiday".split("+"))

이를 그림으로 표현하면 다음과 같습니다.

2. 인과 효과 정의 (Identifying causal effect)

이 단계에서는 앞에서 정의한 인과 모형에 identify_effect함수만 사용하면 됩니다.

1	rainy_identified = rainy_effect.identify_effect()

3. 인과 효과 추정 (Estimating causal effect)

모형을 구축했으면 이제 propensity score를 이용한 matching과 stratification 방법으로 인과 효과 (ATT)를 계산할 수 있습니다.

Matching은 backdoor.propensity_score_matching을,
Stratification은 backdoor.propensity_score_stratification을 이용해 추정합니다.

rainy_matching = rainy_effect.estimate_effect(rainy_identified,method_name = "backdoor.propensity_score_matching")
rainy_stratify = rainy_effect.estimate_effect(rainy_identified,method_name = "backdoor.propensity_score_stratification")

print("Causal Estimate of Matching: {}".format(rainy_matching.value))
print("Causal Estimate of Stratification: {}".format(rainy_stratify.value))

그 결과는 어떻게 나왔을까요?

1 2	Causal Estimate of Matching: -5.973268418151754 Causal Estimate of Stratification: -10.434986509124656

Matching의 결과는 비가 올 때는 오지 않을 때보다 대여량이 평균 5.97회 정도 준다고 말하고 있고, Stratification의 결과는 평균 10.44회 준다고 말하고 있습니다.

이렇게 결과가 나온 이유에 대해 추측해보자면…

propensity score를 추정하는 모형에서 iteration이 최대횟수에 도달했기 때문에 최적의 추정값이 아닐 수 있습니다. 아래 사진처럼 WARNING이 떴었는데 로지스틱 회귀를 돌리는 동안 수렴을 하지 않는 것 같습니다. max_iter를 늘려보려 했지만 dowhy패키지 함수에서 옵션으로 정해놓은 것 같지 않네요 ㅜㅜ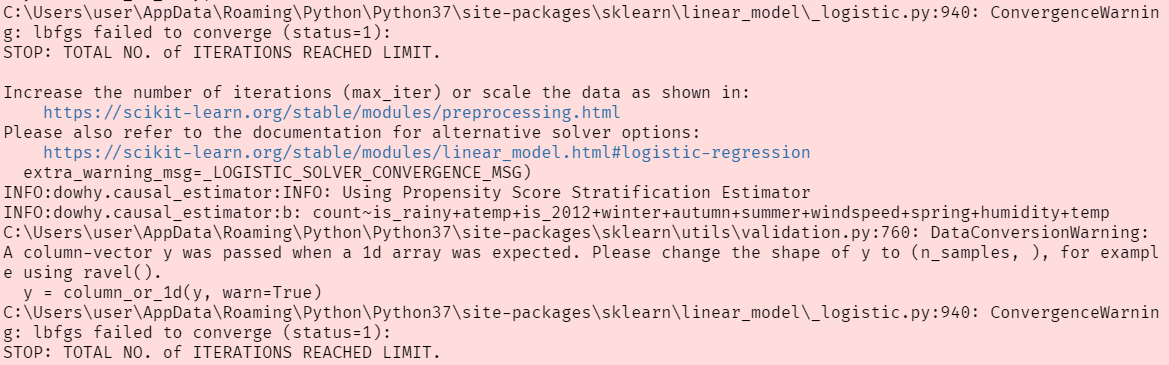
제가 선정한 교란변수인 common_causes나 effect_modifiers가 실제 구조와 다를 수 있습니다. 즉, 제가 가정한 변수들 간의 관계가 다르게 설정되어 있으면 인과 관계 추정값이 명확하지 않을 수 있습니다.
단순 Matching과 Stratification 방법 간 차이일 수도 있습니다.

4. 추정값 반박 (Refuting the estimate)

따라서, 인과관계 추정이 잘 된 게 맞는지 확인하는 절차가 필요합니다. 이는 “Sensitivity Analysis” (민감도 분석)이라고도 하는데요.

추정값을 반박을 통해 새로 추정된 인과효과가 기존의 추정값과 비슷하다면 추정이 잘 되었다라고 말할 수 있습니다. dowhy에서는 이런 방법으로 세 가지를 소개합니다.

무관한 교란 변수 생성
가짜 처리 생성
데이터 중 일부만 추출 후 인과관계 추정

따라서 저도 두 가지 추정방법(matching, stratification)에 따른 세 가지 반박 방법을 모두 시행해보았습니다.

rainy_random    = rainy_effect.refute_estimate(rainy_identified, rainy_matching,method_name="random_common_cause") # 1. 무관한 교란변수 생성
rainy_placebo   = rainy_effect.refute_estimate(rainy_identified, rainy_matching,method_name="placebo_treatment_refuter", placebo_type="permute") # 2. 가짜 처리 생성
rainy_subset    = rainy_effect.refute_estimate(rainy_identified, rainy_matching,method_name="data_subset_refuter", subset_fraction=0.8) # 3. 일부만 추출


rainy_random_str    = rainy_effect.refute_estimate(rainy_identified, rainy_stratify,method_name="random_common_cause")
rainy_placebo_str   = rainy_effect.refute_estimate(rainy_identified, rainy_stratify,method_name="placebo_treatment_refuter", placebo_type="permute")
rainy_subset_str    = rainy_effect.refute_estimate(rainy_identified, rainy_stratify,method_name="data_subset_refuter", subset_fraction=0.8)

print(rainy_random)
print(rainy_placebo)
print(rainy_subset)
print(rainy_random_str)
print(rainy_placebo_str)
print(rainy_subset_str)

Refute: Add a Random Common Cause
Estimated effect:(-5.973268418151754,)
New effect:(-10.403545838691898,)

Refute: Use a Placebo Treatment
Estimated effect:(-5.973268418151754,)
New effect:(-6.113356604813522,)

Refute: Use a subset of data
Estimated effect:(-5.973268418151754,)
New effect:(-9.094270295097026,)

Refute: Add a Random Common Cause
Estimated effect:(-10.434986509124656,)
New effect:(-21.301415881273474,)

Refute: Use a Placebo Treatment
Estimated effect:(-10.434986509124656,)
New effect:(4.483875208301899,)

Refute: Use a subset of data
Estimated effect:(-10.434986509124656,)
New effect:(-20.62884261683204,)

이처럼 Matching의 경우 refuting을 통해 새로 추정된 New Effect의 값은 기존의 값인 Estimated effect와 5 정도 차이나고, Stratification의 경우 14 정도나 차이납니다.
이 데이터에서는 Matching이 더 robust한 결과를 내고 있기 때문에 더 신뢰할 만합니다.

What’s Next?

이 포스팅에서는 Matching과 Stratification에 따른 인과관계 추론 방법에 대해 정리하고, 공유 자전거 데이터를 바탕으로 인과관계를 추정해보았습니다.
인과 추론에 대한 더 쉬운 예제를 보려면 카카오 데이터분석가 이민호님 발표: Causal Inference [link]를 참고하시면 좋습니다.

데이터를 분석해보며 든 생각은

추정치 반박 (Refuting estimates) 부분에서 얼마나 효과 차이가 적어야 robust하다 말할 수 있는 지 기준이 없고
Matching과 Stratification에서 Propensity score를 추정하는 방법을 로지스틱이 아니라 더 성능이 좋은 기계학습 모형을 쓰면 좋겠다는 생각과
배경지식만으로 변수들 간의 관계를 파악하지 않고 구조를 체계적으로 학습하는 내용이 필수적이라는 점입니다.

따라서 다음에는

여러 기계학습 모형을 통해 인과관계를 추정하는 causalml 패키지와
변수 간의 관계를 파악하기 위한 causalnex 패키지

를 사용해서 인과관계를 더 심도있고 정확하게 추론해보고자 합니다.

References

블로그 / 발표
- 카카오 데이터분석가 이민호님 발표: Causal Inference [link]
- Amit Sharma, Emre Kiciman님의 gitbook[link]
파이썬 패키지
- Python dowhy Documentation [link]
- Python causalml Documentation [link]
- Python causalnex Documentation [link]
데이터
- kaggle의 Bike Sharing Demand 데이터[link]