AdaBoost에 대한 자세한 설명

Posted on 2020-08-14 Edited on 2023-05-20 In machine-learning

Bagging과 Boosting의 원리를 정리한 지난 포스팅에 이어 이번에는 Boosting을 기반으로 한 AdaBoost에 대해 정리했습니다.

Bagging과 Boosting의 원리를 정리한 지난 포스팅에 이어 이번에는 Boosting을 기반으로 한 AdaBoost에 대해 정리했습니다.

AdaBoost의 원리

AdaBoost는 Adaptvie Boosting의 준말로, 분류 결과가 틀린 부분 (오류)을 개선해나가는 방향으로 업데이트됩니다.

예를 들어 위의 그림처럼 나무 모형 3개를 이용한다면

나무 모형 1에서 binary하게 예측합니다. 이렇게 하나의 노드만 가진 나무 모형을 stump^{나무의 그루터기, 밑동}라 부릅니다.
나무 모형 2는 나무 모형 1이 잘못 예측한 데이터를 더 잘 분류하도록 가중치를 크게 주어 분류합니다.
나무 모형 3은 나무 모형 1, 2가 잘못 분류한 데이터를 더 잘 분류하도록 가중치를 크게 주어 분류합니다.
마지막으로, 3개의 모델별로 가중치를 계산해 최종 분류 모형을 생성합니다.

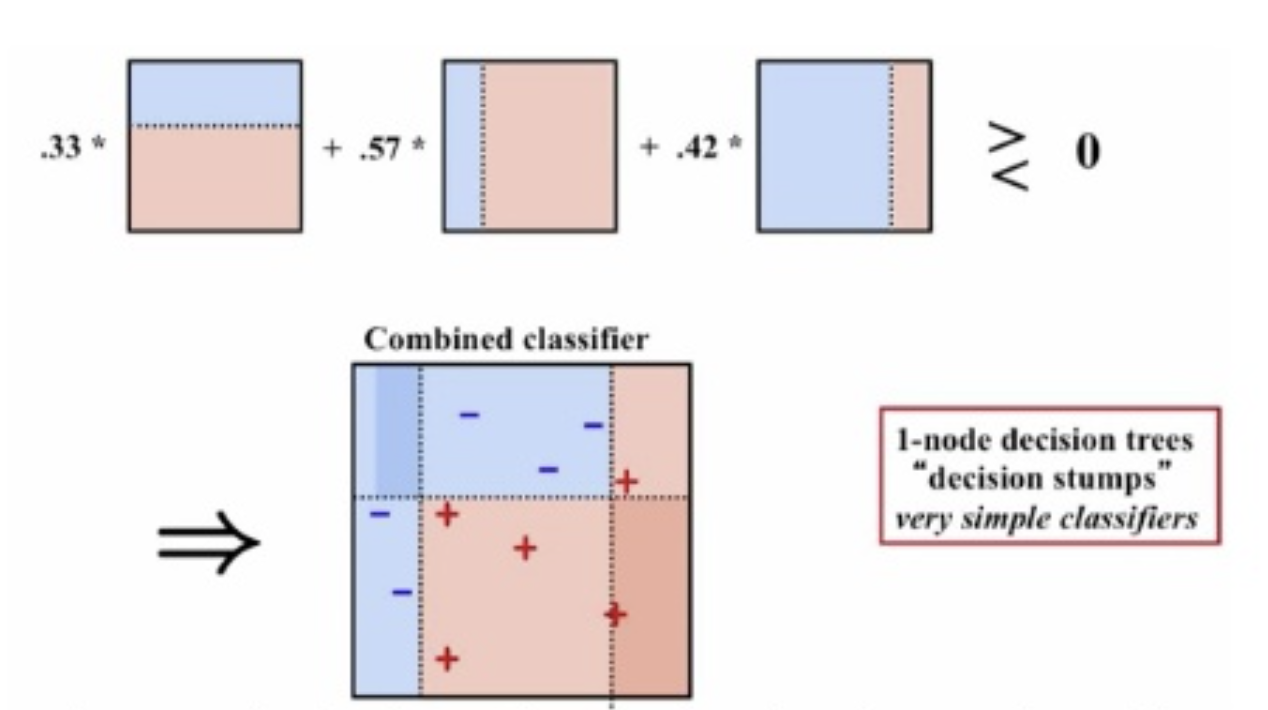
그러면 데이터 별 가중치와 모델 별 가중치를 어떻게 계산할까요?

AdaBoost의 데이터별 & 모델별 가중치 계산 방법

AdaBoost에서 최종 분류 식은 다음과 같이 $T$ 개의 나무 모형 예측값 $f(x)$ 의 가중합으로 주어집니다.

F(x) = \text{sign} (\sum_{t=1}^{T} \alpha_t f_t(x))

여기서

$f_t(x)$ 는 $t$ 번째 약한 학습기(weak learner)로 예측한 $y$ 값을 의미하고
$\alpha_t$ 은 $t$ 번째 학습 결과에 곱해지는 가중치를 의미합니다.
마지막에 $\text{sign}$ 로 $\sum_{t=1}^{T} \alpha_t f_t(x)$ 의 값이 양수이면 1, 음수이면 -1을 출력해 예측 결과를 냅니다.

만약 데이터가 $n$ 개의 샘플을 가졌고 $x_i \in \mathbb{R}^d$ , $y_i \in \{-1,1\}$ 이라 할 때 AdaBoost의 가중치 계산 과정은 다음과 같습니다.

모든 샘플에 똑같은 가중치를 주어 가중치를 초기화합니다.
$D_1(x_i, y_i) = \frac{1}{n},\ i=1,\ldots,n$
$t=1,\ldots,T$ 번째 반복마다
1. 오차 계산
  $\varepsilon_t = \frac{\text{잘못 분류한 데이터 개수}}{전체 데이터 개수} = E_{w_{t}} [1_{y \neq f(x)}]$
2. $t$ 번째 약한 학습기에 곱해지는 가중치 $\alpha_t$ 을 다음과 같이 계산합니다.
  
  $\alpha_t = \frac{1}{2} \ln \left( \frac{1-\varepsilon_t}{\varepsilon_t}\right)$
  
  이 $\alpha_t$ 의 생김새는 다음과 같습니다.
  
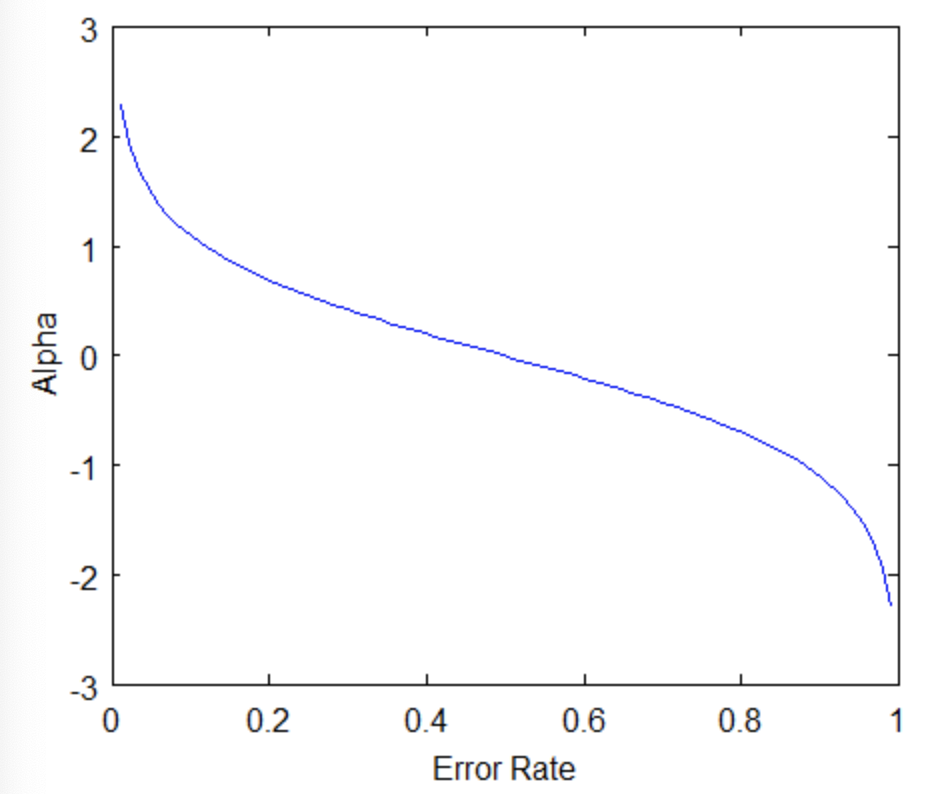
  이 생김새를 바탕으로 약한 학습기의 가중치를 왜 이렇게 정했는 지 직관적으로 파악할 수 있습니다.
  - $\varepsilon \rightarrow 0$ 이면 $\alpha_t$ 는 기하적으로 커집니다. 즉 오류가 적으면 그 모형은 더 많은 가중치를 받게 됩니다.
  - 만약 $\varepsilon = 0.5$ 이면 $\alpha_t = 0$ 입니다. 50%의 정확도를 가진 분류기는 random guess (무작위로 때려 맞추는 것)과 같기 때문에 무시합니다.
  - $\varepsilon \rightarrow 1$ 이면 $\alpha_t$ 는 음수 방향으로 커집니다. 이 말인 즉슨, 50%보다 오차가 크면 분류를 잘못하고 있는 것이기 때문에 그 분류기의 결과에 반대되는 결과를 도출하도록 가중치를 조정하는 것입니다.
3. $t$ 번째 훈련 데이터의 가중치를 다음과 같이 계산합니다.
  $D_{t+1} (i) = \frac{D_t (i) \exp (-\alpha_t y_i f_t (x_i))}{Z_t}$
  가중치 $D(i)$ 를 분포로 이해하면, $D(i)$ 는 다음 훈련 데이터에 $i$ 번째 값이 포함될 확률로 이해할 수 있습니다. 분포라는 특성 상 모든 확률들을 더하면 1이되어야 하기 때문에 정규화 상수 (normalizing factor)인 $Z_t$ 를 나누어줍니다.
  
  여기에 인덱스 $i$ 가 붙은 이유는 각 훈련 샘플별로 이 값을 계산해줘야하기 때문입니다. 왜 가중치가 이렇게 되는 지 설명하자면 다음과 같습니다.
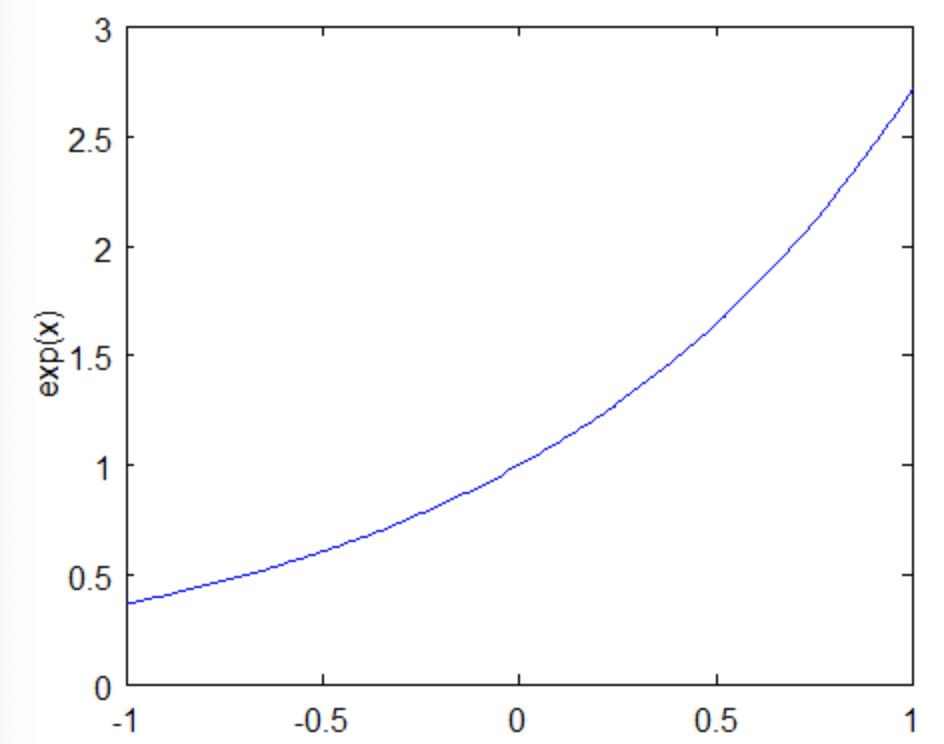
- 지수 함수 $\exp(x)$ 는 다음과 같이 $x$ 가 음수이면 1보다 작은 양수 값을 갖고, 양수이면 1보다 크거나 같은 값을 갖습니다.
- 따라서 $i$ 번째 샘플의 가중치는 $-\alpha_t y_i f_t (x_i)$ 의 부호에 따라 작은 값을 갖거나 큰 값을 갖게 됩니다.
- 근데 $y_i$ 는 $-1$ 이거나 $1$ 이고, $f_t(x_i)$ 는 $t$ 번째 나무가 분류한 $y$ 값을 의미하므로 결국 $y_i f_t(x_i)$ 도 $-1$ 이거나 $1$ 의 값을 갖습니다. 더 자세하게는 $y \neq f_t(x_i)$ 이면 $y_i f_t(x_i) = -1$ 이고, $y=f_t(x_i)$ 이면 $y_i f_t(x_i) = 1$ 이됩니다.
- 결과적으로, 양의 $\alpha$ 값을 갖고, 잘못 분류된 관측치는 더 많은 가중치로 업데이트 됩니다.
마지막으로 이들의 결과를 합산해 $F_t(x)$ 를 계산합니다.

이러한 AdaBoost는 과적합에 덜 민감하고, 예측력도 좋은 모형이라 알려져 있습니다. 개개인의 학습기는 설명력이 약할 수 있어도 이 학습기의 성능이 그냥 random guess보다 좋다면 이들이 합쳐졌을 때 더 강력한 학습기를 생성할 수 있습니다. 그러나 설명력이 약한 noisy한 데이터나 이상치에 민감하다는 단점이 존재합니다.

AdaBoost in Python

이번에는 파이썬으로 AdaBoost를 iris 데이터에 적용한 예를 보여드리고자 합니다.

파이썬 패키지 중 sklearn에 AdaBoostClassifier를 이용해 적합하면 됩니다.
참고로 AdaBoostClassifier에 들어가는 주요 hyperparameter들은 다음과 같습니다.

base_estimators: 학습에 사용할 알고리즘
n_estimators: 약한 학습기의 갯수
learning_rate: 학습을 진행할 때마다 적용하는 학습률

from sklearn.ensemble import AdaBoostClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import metrics
#데이터 로드
iris = datasets.load_iris()
X = iris.data
y = iris.target

# train과 test분리
X_train, X_test, y_train, y_test = train_test_split (X,y, test_size = .3)

# AdaBoost 적합
abc = AdaBoostClassifier(n_estimators=50, learning_rate = 1)
model = abc.fit(X_train, y_train)

# 예측
y_pred = model.predict(X_test)

# accuracy 계산
print("Accuracy", metrics.accuracy_score(y_test, y_pred))

이렇게 계산한 정확도는 0.93정도로 높은 정확도를 보이네요!!

쉽게 sklearn을 사용하면 AdaBoost를 사용할 수 있지만 의미와 원리를 이해하는 게 참 중요하다는 생각이 듭니다.
이렇게 AdaBoost도 격파-!했씁니다. ㅎㅎ

References

Chris McCormick의 AdaBoost Tutorial [link]
scikit-learn 튜토리얼 [link]
박상원님의 boosting 기법의 이해 (bagging vs boosting) 발표 [link]
Saucecat의 Boosting Algorithm: AdaBoost [link]