배깅 (Bagging)과 부스팅 (Boosting)의 원리

Posted on 2020-08-06 Edited on 2023-05-20 In machine-learning

자주 & 편히 쓰는 배깅과 부스팅 기반의 나무 알고리즘, 그 원리에 대해 자세히 설명하실 수 있으신가요? 이는 데이터 분석 직군 면접에서 묻는 단골 소재이기도 한데요 (실제 면접 본 곳의 100%가 랜덤포레스트의 원리에 대해 설명하라 했었습니다 (...)). 이에 대한 개념을 차근차근 알아보고자 포스팅을 쓰게 되었습니다.

자주 & 편히 쓰는 배깅과 부스팅 기반의 나무 알고리즘, 그 원리에 대해 자세히 설명하실 수 있으신가요?
이는 데이터 분석 직군 면접에서 묻는 단골 소재이기도 한데요 (실제 면접 본 곳의 100%가 랜덤포레스트의 원리에 대해 설명하라 했었습니다 (…)). 이에 대한 개념을 차근차근 알아보고자 포스팅을 쓰게 되었습니다.

Introduction

배깅과 부스팅을 알아보기 전에 앙상블 학습에 대한 개념을 알아야 합니다. 앙상블 학습 (Ensemble Learning)이란 여러 개의 분류기 (Classifier)를 생성하고 그 예측을 결합해 단일 분류기보다 정확한 최종적 예측을 도출해내는 기법을 의미합니다.

앙상블 학습의 유형은 크게 세 가지입니다 (그 외에도 스태킹을 포함한 다양한 앙상블 방법이 있다고 합니다).

보팅 (Voting)
배깅 (Bagging)
부스팅 (Boosting)

나무 알고리즘 중 랜덤 포레스트 (Random Forest)는 배깅, 나머지 Gradient Boosting, Light GBM, XGBoost는 모두 부스팅을 이용한 방법입니다.
그렇다면 배깅, 부스팅은 어떤 방법을 의미할까요?

배깅 (Bagging)

**배깅 (Bagging)**은 Bootstrap + Aggregating의 합성어로, "부트스트랩 샘플을 합친다!"라고 한 마디로 말씀드릴 수 있습니다. **부트스트랩 (Bootstrap)**이란 원래 통계학에서 표본 분포 (Sampling Distribution)을 구하기 위해 데이터를 여러 번 복원 추출 (resampling)하는 것을 의미합니다.

평균이 $\overline{X}$ 이고, 분산이 $\sigma^2/n$ 인 서로 독립인 $n$ 개의 데이터 $X_1,\ldots X_n$ 가 있을 때 이를 하나의 표본 (samples)이라 부릅니다. 그리고 보통 모집단 (population)의 모평균과 모분산을 추정하기 위해 표본 분포를 구합니다.
근데 표본 분포를 구하려면 또 $n$ 개의 표본들을 여러 개 구해야 하는데 사실상 쉽지가 않은 과정이죠.

이런 한계를 극복하기 위해 나온 과정이 부트스트랩입니다. 하나의 표본을 가지고 $B$ 번 복원 추출 (resampling) 한다면 이 부트스트랩 샘플들의 분포가 표본 분포로 근사된다는 것이 핵심입니다.

자, 그럼 부트스트랩 샘플들을 어떻게 추출하는 지 그림을 통해 알아봅시다.
예를 들어 1,2,3,…,0까지의 값을 가진 $n=10$ 개인 하나의 표본이 있을 때 이 표본으로 $B=3$ 개의 부트스트랩 샘플을 추출하면 다음과 같습니다.

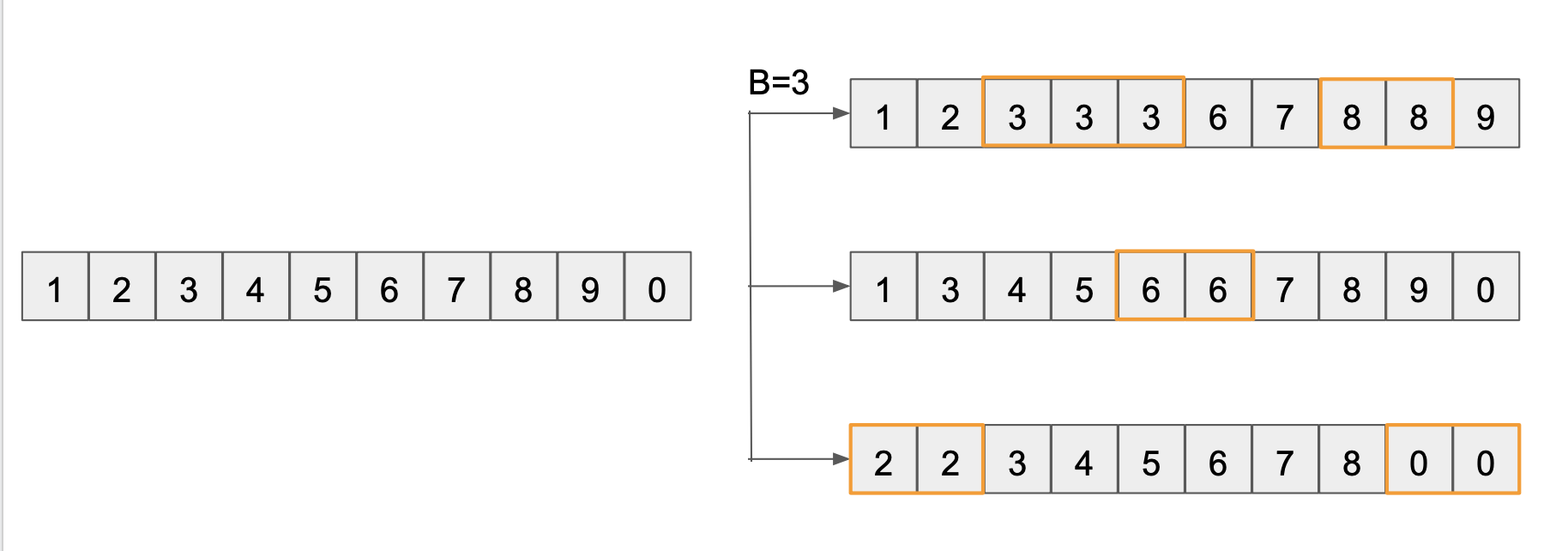
오른쪽의 세 개의 부트스트랩 샘플들은 왼쪽의 데이터 개수와 동일하지만, 개별 데이터가 중복되는 특징이 있습니다. 이렇게

표본 크기와 똑같이 $B$ 번
복원 추출 (with replacement)
하는 것이 부트스트랩 샘플의 특징입니다.
만약 표본 평균을 구하는 것을 목표로 한다면 $B$ 번 추출한 부트스트랩 샘플들의 평균 $B$ 개들의 평균으로 근사할 수 있습니다.

즉, 위의 예에서 3개의 부트스트랩 샘플에서 나온 평균 5, 4.9, 4.6의 합을 $B=3$ 으로 나누어주면 표본평균을 4.83으로 근사하게 됩니다.

이러한 철학을 나무 모형에 적용한 게 배깅이고, 배깅을 이용한 대표적인 나무 알고리즘은 랜덤 포레스트입니다.
랜덤 포레스트가 분류기를 만드는 과정은 다음과 같습니다.

$N$ $N$ 개의 관측치와 $M$ $M$ 개의 피처를 가진 데이터가 있다 할 때 $B$ $B$ 개의 부트스트랩 샘플을 추출합니다. 각 샘플은 중복 추출된 샘플입니다.
- 여기서 부트스트랩 샘플의 개수인 $B$ 는 sklearn.ensemble.RandomForestClassifier의 n_estimators로 조절하고 기본값은 100입니다.
- 또한 각 부트스트랩 샘플의 크기는 max_samples로 조절하고, default는 데이터 개수인 $N$ 입니다.
각 샘플에서 $M$ $M$ 개의 피처 중 랜덤하게 $d$ $d$ 개를 선택합니다. $d$ $d$ 는 보통 전채 피처 개수 $M$ $M$ 의 제곱근으로 주어집니다. 예를 들어 16개의 피처가 있다면 랜덤하게 4개의 피처를 선택합니다.
- $d$ 는 max_features를 통해 조절합니다.
이를 이용해 $B$ 개의 의사 결정 나무를 개별적으로 학습하고 최종적으로 모든 분류기가 보팅을 통해 가장 많이 나온 라벨로 예측을 합니다.

랜덤포레스트가 부트스트랩 샘플로 학습한 나무들의 예측 결과를 합치는건 알겠는데… 왜 2.의 과정처럼 랜덤하게 일부의 피처를 선택할까요?
일부의 피처를 선택하지 않고 모든 피처를 사용한다면 과적합 (overfitting) 문제가 있기 때문입니다.

만약 피처가 16개인데 그 중 한 4개 정도만 유의미한 (dominating) 피처이고 나머지는 예측하는 데 큰 도움이 되지 않는 피처라 가정해봅시다.
16개의 피처를 모두 이용해서 부트스트랩 샘플 개수만큼 ( $B$ 개) 의사 결정 나무를 학습하게 되면 결국 모든 학습 결과에 들어가는 분류 기준은 피처 4개만 관련이 있을 것이고 학습한 나무들은 다 비슷비슷하니까 상관관계(correlation)은 높아집니다. 이런 비슷한 나무들로 예측 결과를 내면 하나의 나무로 예측하는 것과 마찬가지로 높은 분산값을 갖게 되고 과적합 문제를 야기합니다.

따라서 랜덤 포레스트는 각 학습할 나무마다 랜덤하게 피처들을 선택해서 약한 설명력을 가지지만 상관관계는 낮은 나무들을 학습해 이들의 결과를 추합합니다.

Boosting

부스팅은 배깅과 달리

additive training
sequential training

라는 말이 항상 붙습니다. additive하다는 말은 여러 나무들을 합한다는 것을 의미하고, sequential이라는 의미는 여러 나무들을 동시에 학습하지 않고 한 나무가 학습된 결과를 바탕으로 더 나은 결과를 위해 다시 두 번째 나무를 학습하고, 이 두 나무들보다 나은 결과를 위해 세 번째 나무를 학습하는 등 순서대로 학습한다는 의미를 내포합니다.

이렇게 순서대로 학습해 이전 나무에서 잘못 분류한 관측치에 대해 그 다음 나무에서는 더 잘 학습하도록 하도록 합니다. 따라서, 다음 나무에서 관측치가 나타날 확률은 같지 않고, 가장 큰 오차를 보인 관측치들이 나타날 확률이 높도록 가중치를 설정합니다. 즉, 위의 배깅처럼 부트스트랩 샘플들의 각 관측치가 랜덤하게 뽑히지 않고, 오차에 기반해 관측치를 뽑는다는 점에서 차이가 있습니다.

이러한 부스팅의 원리를 사용한 알고리즘은 크게

AdaBoost
Gradient Boosting Model (GBM)
XGBoost

가 있는데요. 이에 대해서는 다음 포스팅에서 자세히 다루겠습니다.