CausalImpact로 COVID-19 데이터를 분석해보자

Posted on Edited on In
이번 포스팅은 Google이 2015년에 발표한 CausalImpact 방법론을 바탕으로 한국의 코로나 확진자수 데이터를 적용시켜본 글입니다.,구체적으로는 한국 사회에서의 코로나를 생각해보면 사회적 거리두기 정책이나 N차 유행인 시기가 있었는데요. "사회적 거리두기가 강화된 시기에 효과가 있었을까?" 혹은 "N차 유행 때 특정 사건으로 인해서 코로나가 얼마나 확산되었을까?"에 대한 답을 가볍게 파악해보았습니다.
  • 이번 포스팅은 Google이 2015년에 발표한 CausalImpact 방법론을 바탕으로 한국의 코로나 확진자수 데이터를 적용시켜본 글입니다.
  • 구체적으로는 한국 사회에서의 코로나를 생각해보면 사회적 거리두기 정책이나 N차 유행인 시기가 있었는데요. “사회적 거리두기가 강화된 시기에 효과가 있었을까?” 혹은 "N차 유행 때 특정 사건으로 인해서 코로나가 얼마나 확산되었을까?"에 대한 답을 가볍게 파악해보았습니다.

CausalImpact 간단 설명

CausalImpact는 시계열 자료에서 어떤 개입 (Intervention)으로 인한 효과를 파악하기 위한 방법론입니다. 개입이라는 말이 좀 낯설지만, 코로나로 예를 들면 한국에서 사회적 거리두기 정책, 특정한 사건 (Ex. 광복절 집회로 인한 코로나 확산 등)이 개입이 될 수 있습니다.

이 개입 효과를 파악하기 위해 CausalImpact 방법론은 관측된 결과 (Observed outcome)와 개입이 없었다면 생길 가상의 결과 (Expected outcome, Counterfactual) 간의 차이를 계산합니다. 즉, 현재는 사회적 거리두기 완화 정책으로 코로나 확진자수가 몇 명인데, 만약 이 완화 정책이 없었다면 몇 명이 되었을지 가상의 결과를 예측하고, 그 차이를 개입 효과라 보는 것입니다.

이를 위해 CausalImpact에서는 개입 효과를 확인하고자 하는 시계열(Ex. 한국의 사회적 거리두기 정책에 따른 코로나 확진자수)과 개입에 영향받지 않는 대조 대상 (Control)이 되는 시계열 (Ex. 미국의 코로나 확진자수)가 주어졌을 때, 베이지안 구조적 시계열 모형(Bayesian Structural time-series model)을 구축합니다. 이 모형은 트렌드, 계절성을 잡아주는 상태-공간 모형의 일종인데요. 자세한 내용은 역시 논문을 읽어봄이 좋을 것 같습니다 :>

CausalImpact로 COVID-19 데이터 분석하기

이번 글의 핵심은 CausalImpact 패키지로 코로나 확진자수 데이터를 적용해보는 것입니다.
이번엔 오랜만에 제 마더 랭귀지 R을 사용하였습니다.

이를 위해 다음의 라이브러리를 설치하고 불러옵니다.

coronavirus 라이브러리로 확진자수 데이터 불러오기

1
2
3
4
5
6
7
8
library(coronavirus) #데이터를 불러오는 패키지
library(CausalImpact)
library(tidyverse) 
library(lubridate) #날짜 관련 라이브러리

## 데이터 불러오기
data(coronavirus)
df = coronavirus

coronavirus 패키지는 전세계 코로나 정보 데이터를 담고 있습니다.
이 중 한국의 코로나 확진자수 데이터를 가져왔습니다.

1
2
df_kr =  df %>% 
  filter(str_detect(country, 'Korea'), type =='confirmed')

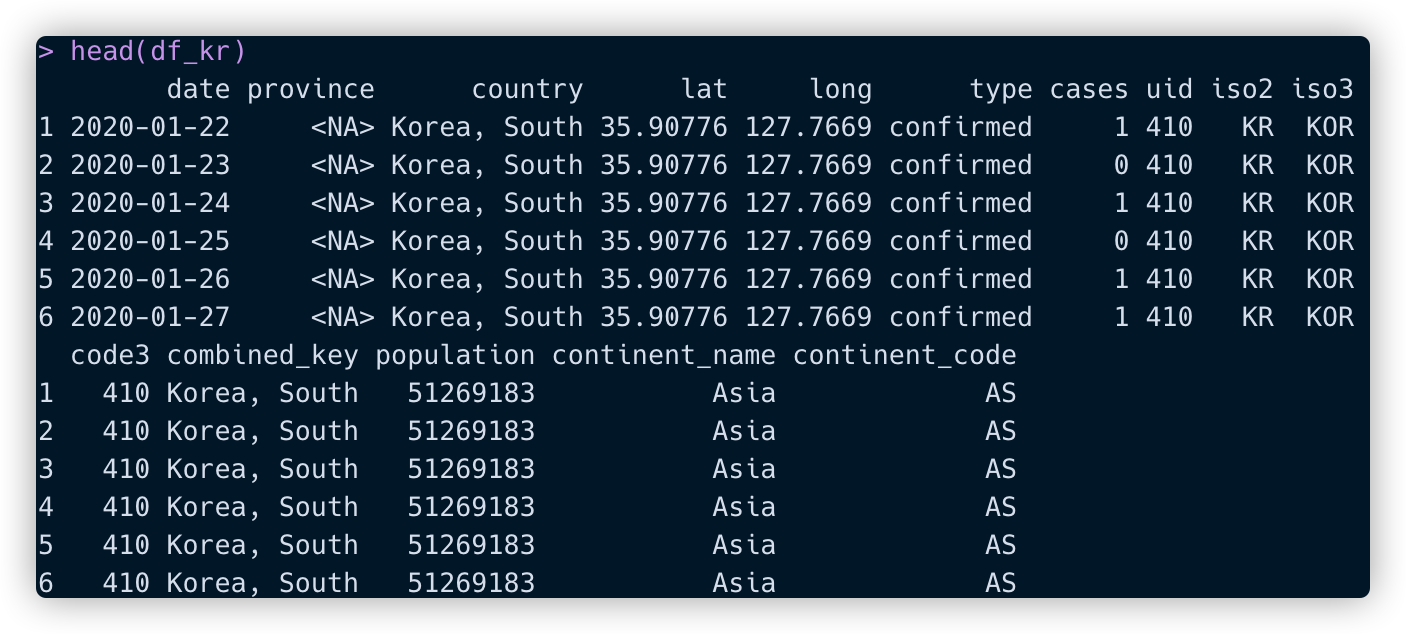
위 데이터는 다음과 같은 컬럼을 갖고 있습니다.

  • date: YYYY-MM-DD 포맷의 날짜
  • province: 주의 이름
  • country: 나라 이름
  • lat: 위도
  • long: 경도
  • type: confirmed (확진) / death (사망) / recovered (회복) 중 하나
  • cases: 해당 날짜의 type에 따른 사람 수
  • uid: 국가 코드
  • iso2: 두 글자로 이뤄진 국가 코드
  • iso3: 세 글자로 이뤄진 국가 코드
  • code3: UN 국가 코드
  • combined_key: 국가와 주 명
  • population: 국가의 인구
  • continent_name: 대륙 명
  • continent_code: 대륙 코드

데이터를 보면 다음과 같습니다.

한국의 코로나 상황 시각화

이 글을 쓰면서 얼마나 많이 코로나와 관련한 거리두기 정책이 있었고, 어떤 유행이 있었는지 곱씹어볼 수 있는 기회가 있었는데요. 킹무위키를 통해 알아낸 수도권 사회적 거리 두기 정책 변화 시점을 시각화해보았습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 한국 데이터만 뽑아보자
df_kr =  df %>% 
  group_by(date,country) %>% 
  filter(str_detect(country, 'Korea')
         ,type =='confirmed') %>% 
  summarise(cases=sum(cases))

# 기본 확진자수 
covid_plot = ggplot(df_kr, aes(x=date, y=cases)) +
  geom_line()+
  # scale_x_continuous(n.breaks=10)+
  scale_x_date(date_labels="%Y-%m",date_breaks = "1 month")+
  theme(axis.text.x = element_text(angle=90))

# 거리두기 정책 날짜
 covid_policy_plot = 
  covid_plot+
  #---------------------------------------------------------------------------------------------
  # 3단계 화: 20.06.28 ~ 20.11.06
  geom_ribbon(data=subset(df_kr, as_date("2020-02-29") <= date & date <= as_date("2020-05-05")), 
            aes(ymin=0,ymax=Inf), fill="red", alpha=0.2) + # 3단계
  geom_ribbon(data=subset(df_kr, as_date("2020-05-06") <= date & date <= as_date("2020-08-15")), 
              aes(ymin=0,ymax=Inf), fill="yellowgreen", alpha=0.2) + # 1단계
  geom_ribbon(data=subset(df_kr, as_date("2020-08-16") <= date & date <= as_date("2020-08-29")), 
              aes(ymin=0,ymax=Inf), fill="yellow", alpha=0.3) + # 2단계
  geom_ribbon(data=subset(df_kr, as_date("2020-08-30") <= date & date <= as_date("2020-09-13")), 
              aes(ymin=0,ymax=Inf), fill="yellow", alpha=0.6) + # 2.5단계
  geom_ribbon(data=subset(df_kr, as_date("2020-09-14") <= date & date <= as_date("2020-10-11")), 
              aes(ymin=0,ymax=Inf), fill="yellow", alpha=0.2) + # 2단계
  geom_ribbon(data=subset(df_kr, as_date("2020-10-12") <= date & date <= as_date("2020-11-18")), 
              aes(ymin=0,ymax=Inf), fill="yellowgreen", alpha=0.2) + # 1단계 (전국)
  #---------------------------------------------------------------------------------------------
  # 5단계 화: 20.11.07 ~ 21.07.11
  geom_ribbon(data=subset(df_kr, as_date("2020-11-19") <= date & date <= as_date("2020-11-23")), 
              aes(ymin=0,ymax=Inf), fill="yellowgreen", alpha=0.8) + # 1.5단계
  geom_ribbon(data=subset(df_kr, as_date("2020-11-24") <= date & date <= as_date("2020-12-07")), 
              aes(ymin=0,ymax=Inf), fill="yellow", alpha=0.3) + # 2단계
  geom_ribbon(data=subset(df_kr, as_date("2020-12-08") <= date & date <= as_date("2021-02-14")), 
              aes(ymin=0,ymax=Inf), fill="yellow", alpha=0.6) + # 2.5단계
  geom_ribbon(data=subset(df_kr, as_date("2021-02-15") <= date & date <= as_date("2021-07-11")), 
              aes(ymin=0,ymax=Inf), fill="yellow", alpha=0.3) + # 2단계
  #---------------------------------------------------------------------------------------------
  # 4단계 화: 20.07.11 ~ 21.10.31
  geom_ribbon(data=subset(df_kr, as_date("2021-07-12") <= date & date <= as_date("2021-10-31")), 
              aes(ymin=0,ymax=Inf), fill="red", alpha=0.3) + # 4단계
  #---------------------------------------------------------------------------------------------
  geom_vline(xintercept=sapply(c("2020-02-29","2020-05-06","2020-08-16","2020-08-30","2020-09-14"
    ,"2020-10-12", "2020-11-19", "2020-11-24", "2020-12-08", "2021-02-15","2021-07-12"),
                               as_date), color = "gray",size=.5)

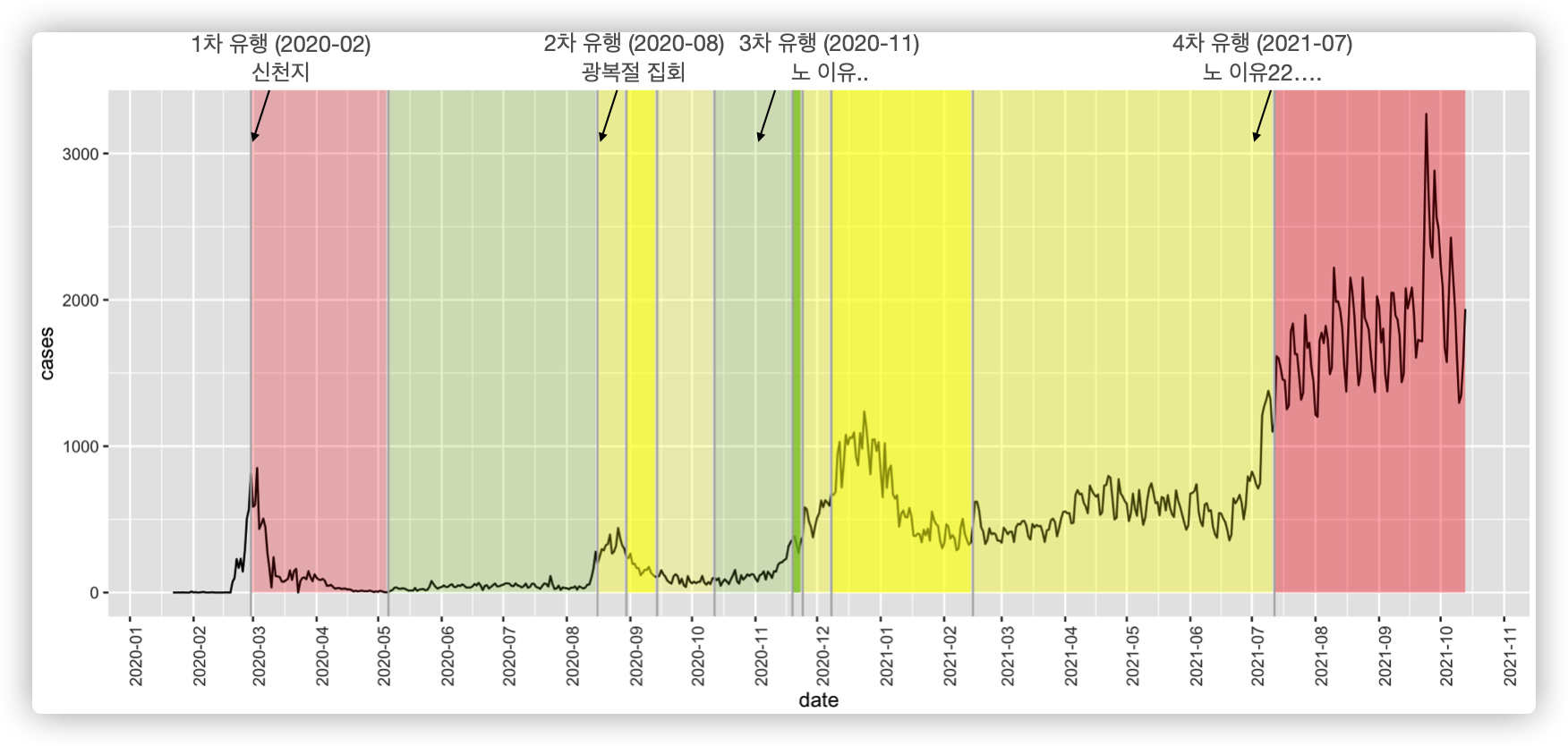
위 그림에서 볼 수 있듯이 색상 (빨강 - 노랑 - 초록)에 따라서 사회적 거리두기 정책의 강도를 표시하고자 하였으며, 색상 내에서도 투명도에 따라서 색이 진하면 같은 단계이지만 정책이 강화되었음을 표기하였습니다. 즉,

  • 초록색 계열의 부분은 사회적 거리두기 정책이 1단계 ~ 1.5단계임을,
  • 노랑색 계열은 2단계 ~ 2.5단계,
  • 빨강색 계열은 3단계 내지는 4단계일 때를 의미합니다.

참고로 지금 시점까지는 없고 2021-10-31 까지의 정책만 나와있어서 이때까지만 그림을 그렸습니다.

또한, 사회적 거리두기 정책은 코로나 확진자수가 많아질 시기에 맞춰서 적용됨을 볼 수 있었는데요. 리서치를 했을 때 한국에서의 코로나 유행은 4차까지 있었습니다.

  • 1차 유행: 신천지, 2020년 2월 ~ 3월
  • 2차 유행: 광복절, 2020년 8월
  • 3차 유행: 2020년 11월 ~ 2021년 1월
  • 4차 유행: 첫 2,000명대 돌파, 2021년 7월 ~

아쉬운 점은 3차 유행 때 정책이 빨리 적용되었어야 할 것 같은데 이에 맞는 정책이 없었다는 점이 보이네요.

이 데이터를 시각화를 통해서 가장 사회적 거리두기 정책이 효과가 있었던 시점은 1차 유행 (2020년 2월 ~ 3월)에 따른 거리두기로 보입니다.
2020년 3월에 851명까지 갔다가 4월 19일에 확진자수가 다시 한 자리수로 돌아왔는데요 ㅜㅜ 이 때가 계속 유지되었으면 어땠을까… 생각이 듭니다…

잘봐 이것이 사회적 거리두기 효과이다!

제가 CausalImpact를 통해 보고 싶었던 것은 코로나 확진자수를 줄이는데 사회적 거리두기 효과가 있었는지 확인하는 것입니다.
이를 위해 CausalImpact 함수에 사용되는 파라미터부터 살펴보았습니다.

  • data: **반응 변수 (response variables)**와 **공변량 (covariates)**으로 이루어진 시계열 자료로, zoo 객체나 벡터, 행렬, 혹은 데이터프레임 형태일 수 있습니다. 여기서 반응 변수란, 우리가 개입 효과를 측정하고자하는 시계열 자료를 의미하고, 공변량들은 개입 효과를 받지 않은 비슷한 성격을 가진 시계열 자료를 의미합니다. CausalImpact에서는 처리를 받은 시계열 자료와 공변량 간의 관계가 개입 전의 기간 (pre-period)에서도 성립되고 개입 후의 기간 (post-period)에도 지속되는 것을 가정하고 있습니다. 이 때 반응 변수는 무조건 첫 번째 컬럼에 와야하고, 공변량은 그 이후 컬럼으로 만들어져야 합니다.
  • pre.period: 개입 전의 기간을 의미합니다. 이 기간은 반응 변수와 공변량 간의 관계를 추정하는 훈련 기간이라고도 볼 수 있습니다.
  • post.perod: 개입 후의 기간을 의미합니다. 이 기간은 반응 변수에 개입이 없었다면 어떤 값을 가졌을지 예측하기 위한 기간이라고도 볼 수 있습니다.

먼저, 첫 거리 두기 정책 기간이었던 2020-02-29 ~ 2020-05-05 (3단계) 간의 인과 효과를 확인해보고자 하였습니다.
따라서 다음과 같이 인자를 두고자 하였습니다.

  • data
    • 반응 변수 (첫 번째 컬럼): 한국의 코로나 확진자수
    • 공변량 (두 번째 ~ 다섯 번째 컬럼): 캐나다, 그리스, 미국, 일본의 코로나 확진자수, 캐나다나 그리스는 한국과 인구가 비슷해서 픽하였고, 이웃나라 일본과 뺄래야 뺄 수 없는 미국도 포함해보았습니다.
    • 이후, zoo 형태로 데이터를 만들어주어야 하는데요. zoo(행렬, 날짜) 형태로 만들어주었습니다.
  • pre.period: 2020년 2월 29일이 개입이 시작한 기간이므로, 2020-01-22 ~ 2020-02-28로 두었습니다.
  • post.period: 개입이 시작한 기간부터 적당히 4월까지 기간을 두어서 2020-02-29 ~ 2020-04-30로 두었습니다.

이를 코드로 짜면 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
start_date = as_date("2020-01-22")
treat_date = as_date("2020-02-28")
treat_date_p1 = as_date(treat_date) + 1 # 그 다음날
end_date   = as_date("2020-05-01")

# 날짜별, 국가별로 group_by하여 확진자수를 더해주고 컬럼별로 국가 정보를 담고 있도록 만들어주기
df_total = df %>% 
  filter(country %in% c('Korea, South','Canada','Greece','US','Japan'), type == 'confirmed') %>% 
  filter(date >= start_date, date <= end_date) %>% 
  group_by(date, country) %>% 
  summarise(cases=sum(cases)) %>% 
  spread(country, cases) %>%     # long to wide
  select(1,5,2,3,4,6) %>%        # 순서 바꿔주기
  rename(Korea = `Korea, South`) # 컬럼명을 Korea, South -> Korea로 바꿔주기

# zoo 형태로 만들어주기
df_causal = zoo(as.data.frame(df_total[,c(2:6)]), df_total$date)

df_total과 df_causal부분을 좀더 자세히 설명드리면,

  • 우선 한국을 포함한 다섯 국가의 확진자수 (type == confirmed)를 가져와서 보고싶은 기간 start_date ~ end_date까지 잘라주었습니다.

  • 다만, 캐나다나 미국의 경우 주(province)별로도 데이터가 나뉘어져 있어서 group_by와 summarise로 국가별로 확진자수 합산 값을 구하였습니다.

  • 이후 spread()함수를 통해서 길게 늘어진 데이터를 옆으로 펼치는 작업을 하였는데요. 이렇게 국가별로 컬럼을 갖도록 하는 함수입니다.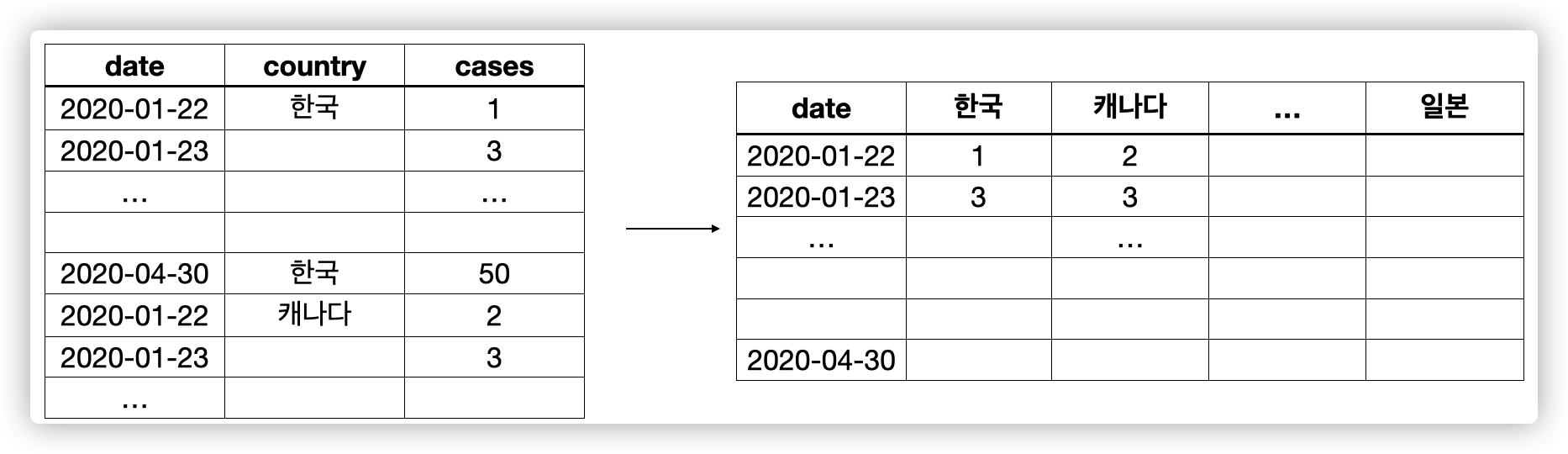

  • 이후 select 함수를 통해 한국 컬럼이 가장 먼저 오도록 하고, rename함수를 통해 국가명을 Korea로 바꿨습니다.

  • 마지막으로 zoo 객체로 만들어주기 위해서 데이터에 해당하는 2번째 ~ 6번째 컬럼을 데이터프레임으로 만들고, date 컬럼을 두번째 인자로 넣어주었습니다.

결과적으로 df_causal 데이터는 이렇게 생겼습니다.

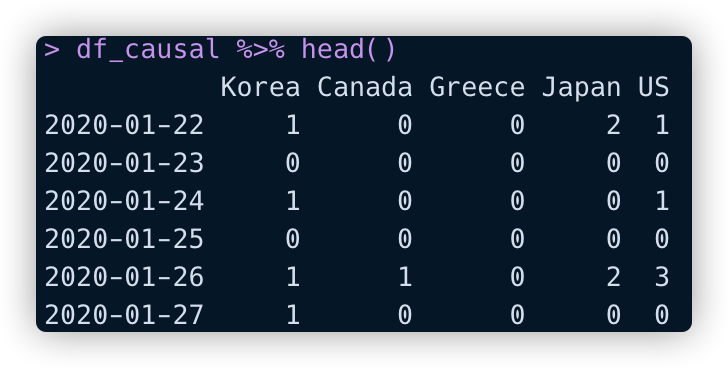
이제 CausalImpact 함수를 적용해서 결과를 해석해보겠습니다.

1
2
3
4
5
6
# CausalImpact 적용하기
causal_impact = CausalImpact(data = df_causal
                             , pre.period = as_date(c(start_date, treat_date))
                             , post.period = as_date(c(treat_date_p1, end_date)))

plot(causal_impact)

위 그림을 보면 original, pointwise, cumulative로 세 개의 패널이 있습니다. 세로로 된 회색 점선은 개입이 시작한 2020-02-29 일자입니다.

  • orginal에서의 검은 실선은 실제 한국의 코로나 확진자수를, 파란색 점선은 만약 사회적 거리두기 정책이 없었다면 나왔을 확진자 수입니다. 즉, 사회적 거리두기 정책으로 인해서 코로나 확진자가 많이 나오지 않았음을 확인하실 수 있습니다.
  • pointwise에서의 파란 점선은 각 시점에서의 개입 효과를 의미합니다. 사회적 거리두기 정책으로 인해서 코로나 확진자수를 감소시키는 효과가 있음을 알 수 있습니다.
  • cumulative에서의 파란 점선은 누적 개입 효과를 의미합니다. 즉, 3월 중순까지는 거의 효과가 0이었지만, 그 이후로 갈수록 개입 효과가 더 커짐을 확인하실 수 있습니다.

이제 summary함수를 통해서 실제 인과 효과를 살펴보겠습니다.

1
summary(causal_impact)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Posterior inference {CausalImpact}

                         Average        Cumulative      
Actual                   136            8437            
Prediction (s.d.)        1858 (978)     115201 (60628)  
95% CI                   [-72, 3771]    [-4444, 233796] 
                                                        
Absolute effect (s.d.)   -1722 (978)    -106764 (60628) 
95% CI                   [-3635, 208]   [-225359, 12881]
                                                        
Relative effect (s.d.)   -93% (53%)     -93% (53%)      
95% CI                   [-196%, 11%]   [-196%, 11%]    

Posterior tail-area probability p:   0.04104
Posterior prob. of a causal effect:  95.896%

For more details, type: summary(impact, "report")

위 표에 대한 줄글로 된 설명을 보고자 한다면 아래와 같이 쓸 수 있습니다.

1
summary(causal_impact,"report")

그러면 아래처럼 행운의 편지 마냥 긴 글을 보게 됩니다. 정신차리고 위 summary 결과에 맞춰 해석해보면 다음과 같습니다.

  • 개입 기간 이후에 한국의 코로나 확진자수 (Actual)는 평균 136명입니다. 만약 사회적 거리두기 정책이 없었다면 1,858명의 확진자수를 가질 뻔 했죠. 이 가상의 예측 (counterfactual prediction)의 신뢰구간은 [-72, 3771]입니다.
  • 개입 기간 이후에 평균적인 인과 효과는 (Abosolute effect) 1,722명입니다. 즉, 사회적 거리두기 정책으로 1,722명을 감소시키는 효과가 있었다 할 수 있습니다.
  • 상대적인 평균 인과 효과 (Relative effect)는 -93%입니다.
  • 또한 누적 효과 (Cumulative) 를 봤을 땐 106,764명을 감소시키는 효과가 있었습니다.

그러나 이 개입 효과가 정말 유의미할까요? 95% CI 부분을 보면 모두 0을 포함하는 것을 알 수 있습니다. 즉, 유의미하게 개입 효과를 추정하고 있다고 말하기 어렵습니다.
이렇게 나온 이유는 아래의 줄 글에서 봤을 때 두 가지로 요약됩니다.

  • 개입 기간이 너무 길거나 짧아서 효과를 제대로 추정하기 어려운 경우도 있고,
  • 혹은 통제가 되는 공변량 (미국, 일본, 그리스, 캐나다)과 한국 확진자수 간의 상관관계가 낮아서 학습하기 어려웠을 수도 있기 때문이라 말하고 있습니다.

결과적으로, 사회적 거리두기 정책의 효과가 잘 나오지 않은 이유는 다음의 두 이유가 가장 클 것 같습니다.

  • 공변량 (네 개의 국가의 코로나 확진자수)들이 반응 변수 (한국의 코로나 확진자수)와 정말 비슷한 흐름을 보이는지 체크를 하지 않았습니다. 실제로 상관관계를 구해보면 -0.2 ~ 0.2 정도의 낮은 상관관계를 가져서 공변량으로 적합하지 않았던 것 같습니다.
  • 다른 국가에서도 분명 비슷한 날짜에 비슷한 사회적 거리두기 정책을 시행했을 수도 있습니다. 그렇기 때문에 "개입을 받지 않았다"고 확실하게 말하기 어려운 것 같습니다.
1
2
3
4
5
6
7
8
9
During the post-intervention period, the response variable had an average value of approx. 136.08. In the absence of an intervention, we would have expected an average response of 1858.08. The 95% interval of this counterfactual prediction is [-71.68, 3770.90]. Subtracting this prediction from the observed response yields an estimate of the causal effect the intervention had on the response variable. This effect is -1722.00 with a 95% interval of [-3634.82, 207.76]. For a discussion of the significance of this effect, see below.

Summing up the individual data points during the post-intervention period (which can only sometimes be meaningfully interpreted), the response variable had an overall value of 8.44K. Had the intervention not taken place, we would have expected a sum of 115.20K. The 95% interval of this prediction is [-4.44K, 233.80K].

The above results are given in terms of absolute numbers. In relative terms, the response variable showed a decrease of -93%. The 95% interval of this percentage is [-196%, +11%].

This means that, although it may look as though the intervention has exerted a negative effect on the response variable when considering the intervention period as a whole, this effect is not statistically significant, and so cannot be meaningfully interpreted. The apparent effect could be the result of random fluctuations that are unrelated to the intervention. This is often the case when the intervention period is very long and includes much of the time when the effect has already worn off. It can also be the case when the intervention period is too short to distinguish the signal from the noise. Finally, failing to find a significant effect can happen when there are not enough control variables or when these variables do not correlate well with the response variable during the learning period.

The probability of obtaining this effect by chance is very small (Bayesian one-sided tail-area probability p = 0.041). This means the causal effect can be considered statistically significant.

마치며

이번 분석은 CausalImpact을 실 데이터에 사용해본 것에 의의를 두며 글을 마무리하려고 합니다.
그 외 많은 사회적 거리두기 정책들이 있었고, 혹은 어떤 트리거로 인해서 1차 유행 ~ 4차 유행이 있었는데 이 트리거의 효과를 보는 것도 의미가 있을 것 같습니다.
(실제로 광복절 집회의 효과를 확인해봤을 때 의미가 있는 결과가 나왔습니다.)

요즘에도 확진자수가 4,000명대를 돌파하며 심상치 않던데… 모두들 건강 잘챙기시고 돌파 감염도 조심하시길 바랍니다.
마스크와 코로나가 없어도 재택이 있는 세상을 꿈꾸며…★