인과 관계 분석 시리즈 (2): 가우시안 베이지안 네트워크 (GBN, Gaussian Bayesian Network)

Posted on 2020-04-12 Edited on 2023-05-20 In bayesian

Gaussian Bayesian Network는 인과 관계를 추론하는 방법 중 하나로, 이전 포스팅에서 설명했습니다.,이번 포스팅에서는 GBN의 구조 학습 및 모형 추정의 원리와 그 예제에 대해 설명드리고자 합니다.

Gaussian Bayesian Network는 인과 관계를 추론하는 방법 중 하나로, 이전 포스팅에서 설명했습니다.
이번 포스팅에서는 GBN의 구조 학습 및 모형 추정의 원리와 그 예제에 대해 설명드리고자 합니다.
전체 코드와 데이터는 이 곳에서 확인하실 수 있고, R 패키지 bnlearn tutorial를 주로 참조했음을 알립니다.

GBN (Gaussian Bayesian Network)

이전 포스팅에서 말씀드렸듯이 Bayesian Network 중 GBN는 노드가 정규분포를 따를 때 쓸 수 있는 방법입니다.

GBN은 데이터로부터 1. 인과 구조를 학습하고 그 구조를 바탕으로 2. 모수를 추정하는 두 단계로 이루어져 있습니다.

모수 추정 (Parameter Tuning)

먼저, 쉬운 2. 모수 추정 방법에 대해 먼저 설명드리겠습니다.
GBN은 $i$ 번째 노드인 $X_i$ 가 local하게 정규분포를 따른다 가정합니다.

X_{i}=\mu_{X_{i}}+\Pi_{X_{i}} \boldsymbol{\beta}_{X_{i}}+\varepsilon_{X_{i}}, \quad \varepsilon_{X_{i}} \sim N\left(0, \sigma_{X_{i}}^{2}\right)

여기서 $\Pi_{X_{i}}$ 는 $X_i$ 의 직계 부모 집합 (a set of direct parents)을 의미합니다.

만약 $X_1, X_2, X_3$ 의 노드에서 인과 관계가 $X_1 \rightarrow X_3$ 와 $X_2 \rightarrow X_3$ 와 같다면,

X_3 = \mu_{X_{3}}+\beta_1 X_1 + \beta_2 X_2 +\varepsilon_{X_{3}}, \varepsilon_{X_{3}} \sim N(0,\sigma^2_{X_{3}})

과 같이 직계 부모인 $\Pi_{X_{3}}=\{X_1, X_2\}$ 들이 설명 변수로, 아이인 $X_3$ 이 반응 변수로 두고 선형 회귀식을 적합합니다. 회귀 계수의 추정은 MLE^{Maximum Likelihood Estimation}을 통해 추정합니다.

Causal Structure Learning

1. 인과 구조를 학습하는 과정은 학습 방법에 따라 크게 세 가지 방법이 있습니다.

Score based: Hill Climbing Algorithm
Constraint based: Grow-Shrink Markov Blanket, Incremental Association, Fast Incremental Association, Interleaved Incremental Association
Hybrid: Max-Min Hill Climbing

Score based는 약간 heuristic한 방법인데요. 선형회귀에서 단계 별로 변수를 선택할 때 AIC나 BIC를 기준으로 최적의 모형을 선택하듯이 score based도 네트워크에서 한 연결 (edge)을 끊어보기도, 붙여보기도 하면서 각 DAG의 score를 비교하는 방식입니다. 마찬가지로 score도 BIC를 사용합니다.

Constraint based는 조건부 독립 검정 (CI; Conditional Independence test)을 통해 인과 관계를 파악하는 알고리즘입니다.

마지막으로 Hybrid은 score based와 constraint based를 적당히 섞은 알고리즘입니다.

저는 여기서 가장 기본이 되는 Score based의 Hill Climbing Algorithm과 Constraint based의 Grow-Shrink Markov Blanket Algorithm에 대해 알아보겠습니다.

Hill Climbing Algorithm

Hill Climbing 알고리즘은 Score에 기반한 방법 중 하나로, BN이 얼마나 데이터 셋 $\mathcal{D}$ 를 잘 표현하고 있는 지를 점수로 표현합니다. DAG 구조를 $\mathcal{G}$ , 데이터 셋을 $\mathcal{D}$ 라 할 때, score는 다음과 같이 정의됩니다.

\operatorname{BICscore}(\mathcal{G}, \mathcal{D})=\log \operatorname{Pr}(\mathcal{D} \vert \mathcal{G})-\frac{d}{2} \log N

여기서 $\log \operatorname{Pr}(\mathcal{D} \vert \mathcal{G})$ 는 $\mathcal{G}$ 의 인과 구조를 가졌을 때의 로그 가능도이고 $d$ 는 free parameter의 개수입니다.

GBN 노드 각각의 분포는 정규분포이니 가능도 또한 정규분포이겠네요! 이 식에서 알 수 있듯이 BIC^{Bayesian Information Criteria}는 높을수록 좋습니다. (참고로, 원래 회귀에서 쓰던 BIC는 로그 가능도에 "-"가 붙어있고 penalty는 양수여서 작을수록 좋습니다.)

이제 이 점수들을 갖고 Hill Climbing 알고리즘은 다음과 같은 순서로 진행합니다.

{: width = “200”, height=“400”}

위는 pseudo code인데 순서에 맞게 설명해보겠습니다.

$\mathcal{E}$ 는 초기 네트워크로, 비었거나 (연결 관계가 없거나) 아예 꽉 차있던가 아니면 랜덤하게 네트워크를 구성
$ProbabilityTable()$ 은 $\mathcal{E}$ 에서 만든 인과 구조 하에서 노드마다 local pdf를 구하고 MLE를 통해 모수들을 추정
첫 BN $\mathcal{B}$ 를 구성 (여기서 $\mathcal{U}$ 는 노드 집합)
score 초기화
반복:
1. maxscore를 score로 둠
2. BN의 쌍 $(X,Y)$ $(X, Y)$ 에 대해서 반복:
  1. 네트워크 구조 $\mathcal{E}$ $E$ 에서
    - $\{X\rightarrow Y\}$ 를 추가해 $\mathcal{E}'$ 에 저장하거나
    - $\{X\rightarrow Y\}$ 를 제거해 $\mathcal{E}'$ 에 저장하거나
    - $\{X\rightarrow Y\}$ 구조를 $\{Y\rightarrow X\}$ 로 반대로 바꿔 $\mathcal{E}'$ 에 저장
    - $\mathcal{T}'$ 에 새롭게 구한 $\mathcal{E}'$ 로 다시 local pdf와 모수를 추정해 저장
  2. 새로운 BN $\mathcal{B}'$ 를 저장
  3. $\mathcal{B}'$ 를 가지고 BIC 점수를 갱신해 newscore에 저장
  4. 만약 newscore가 기존의 score보다 높다면
    - $\mathcal{B}'$ 로 $\mathcal{B}$ 를 갱신하고,
    - score도 newscore로 갱신
newscore가 더이상 갱신되지 않으면 중단
$\mathcal{B}$ 출력

핵심은 각 쌍 $(X,Y)$ 마다 인과관계를 추가해보거나 삭제해보거나 역으로 만들어보는 과정입니다. 이를 그림으로 나타내면 더 이해하기 쉽습니다.

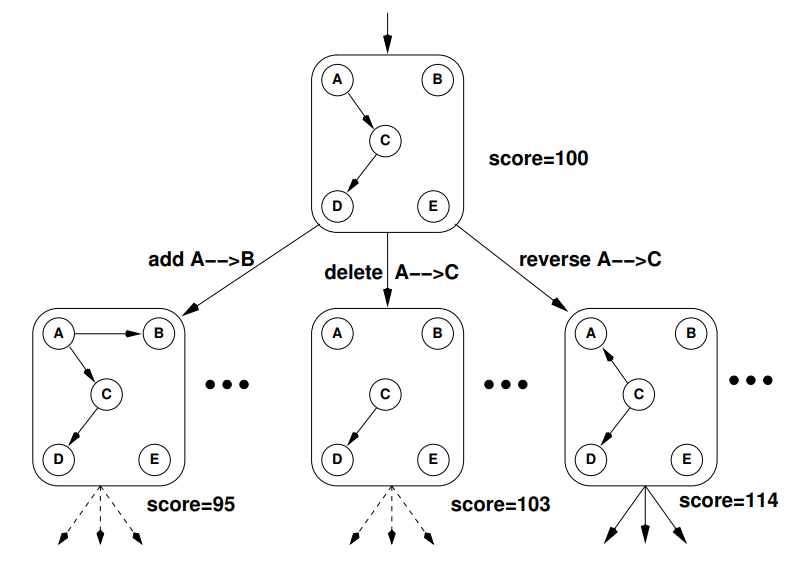
하나의 인과 구조에서 한 엣지씩 붙여보고, 잘라보고, 바꿔보는 과정을 반복해 인과구조를 완성합니다.

Grow-Shrink Markov Blanket Algorithm (GSMB Algorithm)

제가 저번 포스팅에서 Markov Blanket (MB)에 대해 설명은 했지만 왜 이게 중요한 지 잘 이해가 안 갔었는데요. 중요한 이유가 이 알고리즘 때문이었습니다.
다시 설명하자면 Markov Blanket은 세 가지 요소로 이루어져 있습니다.

노드의 직계 부모
노드의 직계 자식
노드의 직계 자식의 부모

이미지 출처: [link]
{:.figure}

앞의 그림에서

$B$ 의 MB는 $\{A, C\}$ ,
$D$ 의 MB는 $\{C, E, F\}$ 가 되겠네요!

이를 수식으로 표현하면 $\mathbf{B}(B) = \{A,C\}$ , $\mathbf{B}(D) = \{C,E,F\}$ 가 됩니다.

MB는 MB를 조건으로 했을 때 다른 노드들은 해당 노드와 조건부 독립이 되는 성질을 가지고 있습니다. 즉 $B$ 의 경우

P(B, E\vert \mathbf{B}(B)) = P(B, D\vert \mathbf{B}(B))=P(B, F\vert \mathbf{B}(B))=P(B\vert \mathbf{B}(B)),\text{where }\mathbf{B}(B) = \{A,C\}

GSMB 알고리즘은 Growing (성장)과 Shrinking (축소)를 통해 노드마다 Markov Blanket을 찾는 게 핵심입니다.

마찬가지로 pseudo code인데요. 설명하자면 다음과 같습니다.

공집합 $\mathbf{S}$ 에서 시작
[성장 단계] $X$ 노드를 제외한 모든 노드 $Y$ 에 대해서 하나씩 반복: $\mathbf{S}$ 를 조건으로 했을 때 $X$ 노드와 $Y$ 독립이 아니라면 $\mathbf{S}$ 에 $Y$ 포함
[축소 단계] $\mathbf{S}$ 에서 한 노드씩 빼가면서 조건부 독립인 지 확인하고, 독립이면 $\mathbf{S}$ 에 $Y$ 제외
X의 markov blanket인 $\mathbf{B}(X)$ 에 $\mathbf{S}$ 저장

이를 그림으로 그리면 다음과 같습니다.

실제 인과 관계 구조는 점선이고, 하나씩 노드를 골라 조건부 독립인 지 확인하는 성장 단계를 거칩니다.
그림에서 보시는 것과 같이 $A$ 의 MB를 구하는 첫 과정으로 $A$ 를 제외한 노드에 대해서 조건부 독립인 지 테스트합니다.

(a)와 (b): 공집합 $\mathbf{S}=\emptyset$ 을 조건으로 했을 때 $A$ 와 $B$ 가 독립인 지 테스트한 과정입니다. 결과적으로 독립이 아니기 때문에 $\mathbf{S}$ 에 $\{B\}$ 가 포함됩니다.
©와 (d): $\mathbf{S}=\{B\}$ 를 조건으로 했을 때 $A$ 와 $F$ 가 독립인 지 확인합니다. 그 결과 독립이기 때문에 $\mathbf{S}$ 는 그대로 유지됩니다.
이를 $A$ 를 제외한 모든 노드에 대해 테스트합니다.

성장 단계가 끝나고 $A$ 의 MB( $\mathbf{S}$ )는 $\{B, G, C, K, D, H, E\}$ 로 구성됩니다.
그 다음에 MB 중 불필요한 노드는 없는 지 확인하기 위해 축소 단계를 거칩니다.

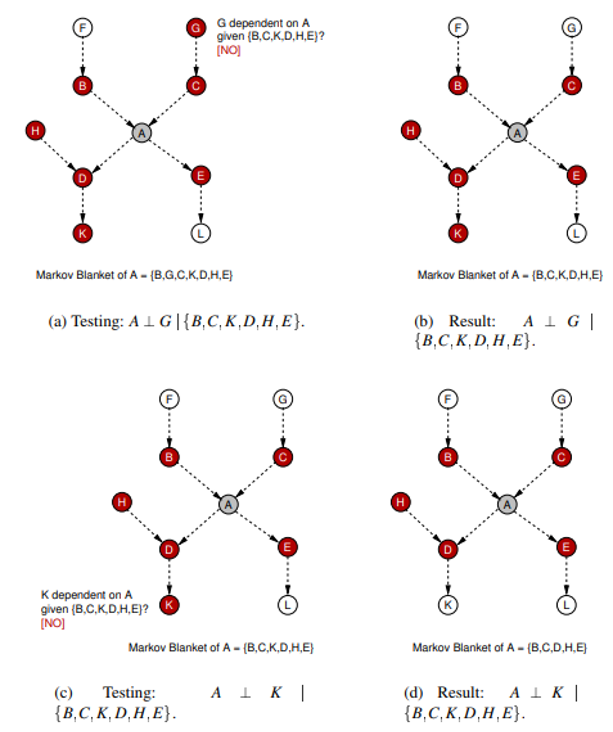
(a)와 (b): 먼저 MB에서 $G$ 를 빼고 조건으로 하여 $A$ 와 $G$ 가 독립인 지 확인합니다. 그 결과 독립이기 때문에 $\mathbf{S}$ 에서 $G$ 를 제외합니다.
©와 (d): 마찬가지로 MB에서 $K$ 를 빼고 조건으로 하여 $A$ 와 $K$ 가 독립인 지 확인합니다. 그 결과 독립이기 때문에 $\mathbf{S}$ 에서 $K$ 를 제외합니다.

최종적으로 성장과 축소 단계를 거쳐 $A$ 의 MB를 $\{B, C, D, H, E\}$ 로 정합니다.

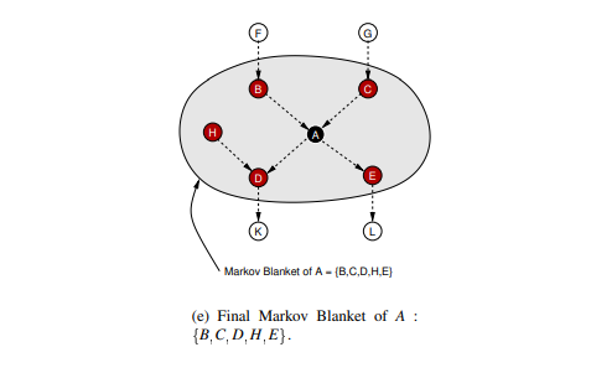
이는 $A$ 노드에 대한 과정이고, $B~L$ 의 노드도 마찬가지로 MB를 구하면 끝입니다.

정리하면…

인과 관계 추론의 핵심은 구조를 학습해서 모수를 추정하는 두 단계, 핵심은 “구조 학습”!
Score based인 Hill climbing 알고리즘은 각 노드의 쌍마다 연결을 끊어보고, 연결해보고, 바꿔보는 과정을 반복해 인과 구조 학습
Constraint based인 Grow-Shrink Markov Blanket 알고리즘은 각 노드마다 성장 단계와 축소 단계를 거쳐 MB를 구해 인과 구조 학습

Data Analysis: Malocclusion Data

이제 이 GBN을 이용해서 실제 데이터를 분석한 예에 대해 알아봅시다.
데이터 출처는 무려 Nature의 Scientific Report 잡지에 실린 Scutari et al. (2017)논문이네요! $(143\times 9)$ 의 작은 데이터입니다.

단어들이 좀 어려운데 핵심은 이겁니다.

$T_1$ 과 $T_2$ 두 시점에 측정된 143명의 부정교합 환자 자료로, 이 두 시점의 차이 (dT)와 부정 교합과 관련한 측정 값들의 차이(dANB~dCoGo)를 변수로 선정하였습니다. 이들은 다음과 같습니다.
- dT: difference in times
- dANB: difference in angle between Down’s points A and B (degrees).
- dIMPA: difference in incisor-mandibular plane angle (degrees).
- dPPPM: difference in palatal plane - mandibular plane angle (degrees).
- dCoA: difference in total maxillary length from condilion to Down’s point A (mm).
- dGoPg: difference in length of mandibular body from gonion to pogonion (mm).
- dCoGo: difference in length of mandibular ramus from condilion to pogonion (mm).
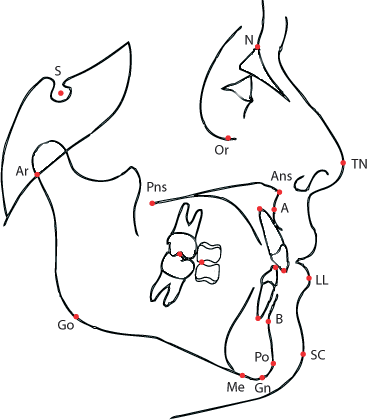
결국 부정 교합과 관련있는 거리나 각도들을 $T_1$ 과 $T_2$ 시점에 측정해서 그 차이들을 변수로 만들었습니다.
범주형 변수는 처리 (Treatment)와 부정교합의 상태 (Growth)입니다. 처리는 받지 않았으면 0, 받았으면 1의 값을 갖고, Growth는 부정교합 상태가 악화됐으면 0, 완화됐으면 1의 값을 갖습니다. 다만 이들을 "연속형"으로 간주하고 GBN에 적용했습니다.
목표는 두 가지로 요약됩니다.
- 기존에 가졌던 가정과 인과 관계 결과가 일치하는 지
- "만약 이 변수가 이 값을 가졌다면 처리 효과는 어떻게 될까?"와 같은 인과 관계 추정

이 데이터를 통해 GBN을 사용하면 다음과 같습니다.

$\varepsilon_{\Delta Y/\Delta T} \sim N\left(0, \sigma_{\Delta Y}^{2}\right), \Delta T=T_{2}-T_{1} , \Delta Y=Y_{T_{2}}-Y_{T_{1}}$ 라 할 때,

\frac{\Delta Y}{\Delta T}=\mu^{*}+\frac{\text { Growth }}{\Delta T} \beta_{G}^{*}+\frac{\text { Treatment }}{\Delta T} \beta_{T R}^{*}+\frac{\Delta X_{1}}{\Delta T} \beta_{2}^{*}+\ldots+\varepsilon_{\frac{\Delta Y}{\Delta T}}

여기서 $\Delta Y$ 는 dANB~dCoGO의 6개 변수에 해당합니다. 이제부터 이 변수를 “안면 관련 변수” (craniofacial features)라 부르겠습니다.

EDA

먼저, 필요한 R 라이브러리입니다.

library(GGally)
library(bnlearn)
library(Rgraphviz)
library(penalized)
library(visNetwork)
library(dplyr)

변수에 대해 잘 모르기 때문에 EDA가 더 중요합니다.

diff로 파일을 불러오고 시간 차이 $\Delta T$ 로 나눠준 자료를 diff_delta에 저장해서 상관 관계와 pairs 플랏을 그려봅니다.
데이터를 부를 때 mutate_if를 쓰는 이유는 bnlearn에서 모형 학습을 하려면 자료형이 integer가 아니라 numeric이어야 하기 때문입니다.

diff=read.csv("dental.csv") %>% 
    mutate_if(is.integer, as.numeric)
diff_delta = cbind(Treatment=diff$Treatment,
                   Growth=diff$Growth,
                   sapply(diff[, 1:6], function(x) x / diff$dT))
ggcorr(diff_delta,palette="RdBu",label=TRUE,label_round=3)
ggpairs(diff[,c("dANB", "dPPPM", "dIMPA", "dCoA", "dGoPg", "dCoGo")])

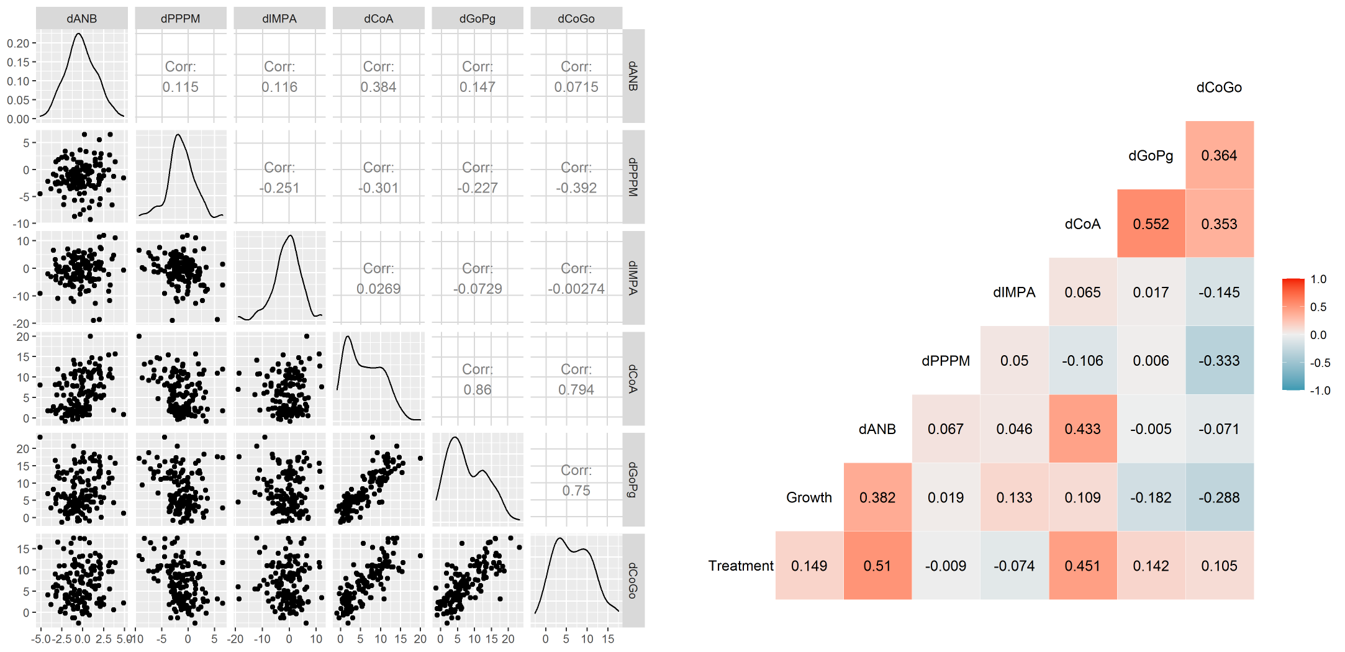
상관관계와 산점도를 보면

dCoGo, dGoPg, dCoA 간의 상관관계
Treatment, dANB, dCOA 간의 상관관계

가 돋보입니다. 산점도도 보면 일직선에 가까운 모습이죠. 특히 Treatment와 dANB, dCOA는 아래 턱점 A와 관련이 있기 때문에 의학적으로 흥미로운 결과라 합니다. 또 처리가 주로 영향을 미치는 변수가 이 두 개라 추측할 수 있습니다.

Step1: Black List and White List

인과 관계 구조를 학습하는 데에 앞서 이어지지 말아야 할 연결을 black list에, 꼭 이어져야 할 연결을 white list에 지정합니다.
Scutari et al. (2017)에서는 다음과 같이 black list와 white list를 지정했습니다.

Black list: 총 22개의 연결을 제외합니다.
- (18개) 안면 관련 변수(dANB~dCoGO)에서 dt, Treatment, Growth로 오는 arc는 모두 제외해야 합니다.
  왜냐하면 시간의 차이(dt)나 처리 (Treatment)로 안면 관련 변수의 측정값이 변화할 수는 있어도 그 반대는 성립하지 않기 때문입니다. 마찬가지로 부정교합의 상태(Growth)에 따라 안면 관련 변수의 측정값이 바뀌는 것이기 때문입니다.
- (2개) 처리(Treatment)는 시간의 차이(dT)의 원인이 될 수 없고 그 반대도 성립하면 안되기 때문에 제외합니다.
- (2개) 부정교합의 상태(Growth)는 처리(Treatment)와 시간 차이(dT)의 원인이 될 수 없습니다.
따라서 black list를 다음과 같이 지정합니다.

$\begin{aligned} \text{안면 관련 변수} &\rightarrow \mathtt{dt}\\ \text{안면 관련 변수} &\rightarrow \mathtt{Growth}\\ \text{안면 관련 변수} &\rightarrow \mathtt{Treatment}\\ \mathtt{Treatment} &\rightarrow \mathtt{dT}\\ \mathtt{dT} &\rightarrow \mathtt{Treatment}\\ \mathtt{Growth} &\rightarrow \mathtt{Treatment}\\ \mathtt{Growth} &\rightarrow \mathtt{dT} \end{aligned}$
White list: 총 3개의 연결을 포함합니다.
- (2개) 사전 지식에 따라 dANB $\rightarrow$ dIMPA $\leftarrow$ dPPPM 연결을 포함합니다.
- (1개) 시간에 따라 부정교합의 상태가 변화해야하므로 dT $\rightarrow$ Growth 연결을 포함합니다.

# DAG에 포함되지 말아야할 엣지들
black_list = tiers2blacklist(list("dT", "Treatment", "Growth",
                                  c("dANB", "dPPPM", "dIMPA", "dCoA", "dGoPg", "dCoGo")))
black_list = rbind(black_list, c("dT", "Treatment"))
# DAG에 포함되어야할 엣지들
white_list=matrix(c("dANB", "dIMPA","dPPPM", "dIMPA","dT", "Growth"),
                  ncol = 2, byrow = TRUE, dimnames = list(NULL, c("from", "to")))

웃긴 건 bnlearn의 패키지에서 black list는 tiers2blacklist 함수를 통해 지정할 수 있는데 white list는 직접 행렬을 만들어줘야 하네요.

Step2: Causal Structure Learning

이제 black list와 white list를 포함해서 Hill-Climbing(HC) 알고리즘과 Grow-Shrink Markov Blanket(GSMB) 알고리즘을 통해 인과 관계를 학습합니다. bnlearn에서는 각각 hs, gs함수를 사용합니다. 이 글에서는 HC 알고리즘을 사용한 결과에 대해서만 리포팅하겠습니다.

1	DAG = hc(diff, whitelist = white_list, blacklist = black_list)

이들의 결과를 보려면 RGraphviz나 visNetwork 패키지를 사용할 수 있습니다. 둘 다 써본 결과
RGraphviz는 사용법이 쉽지만 그래프가 예쁘지 않다는 것이고, visNetwork는 사용법이 조금 복잡하지만 그래프가 예쁩니다.

전 그래서 visNetwork을 사용했고 다음의 함수를 통해 그래프를 그리도록 했습니다.

"plot_network" = function(dag,strength_df=NULL,undirected=FALSE,
                          group=NA,title=NULL,height=NULL,width=NULL)
    {
    edge_size = ifelse(is.null(strength_df),NA,
                   right_join(strength_df, data.frame(dag$arcs[,c(1,2)]))$strength)
    
    nodes = names(dag$nodes)
    nodes = data.frame(id   = nodes,
                       label= nodes,
                       size = 16,
                       font.size= 18,
                       shadow   = TRUE,
                       group    = group)
    
    edges = data.frame(from   = dag$arcs[,1],
                       to     = dag$arcs[,2],
                       value  = edge_size,
                       arrows = list(to=list(enabled=TRUE,scaleFactor=.5)),
                       shadow = TRUE)
    
    if(is.na(group[1]))     nodes = nodes[,-6] # without group
    if(is.na(edge_size)) edges = edges[,-3] # without edge_size
    if(undirected)       edges$arrows.to.enabled=FALSE
    
    network=visNetwork(nodes,edges,main=title,height=height, width=width)%>% 
        visOptions(highlightNearest = TRUE, nodesIdSelection = TRUE)
    return(network)
}

함수의 인자에 대해 간단히 설명드리면 다음과 같습니다.

dag: 인과관계를 학습한 object
strength_df: Bootstrap 후 강도를 나타내는 dataframe
undirected: 방향성이 있는 지의 여부
group: Network 그림에서 쓰이는 그룹
title: Network 그림의 제목
height, width: Network 그림의 높이, 너비

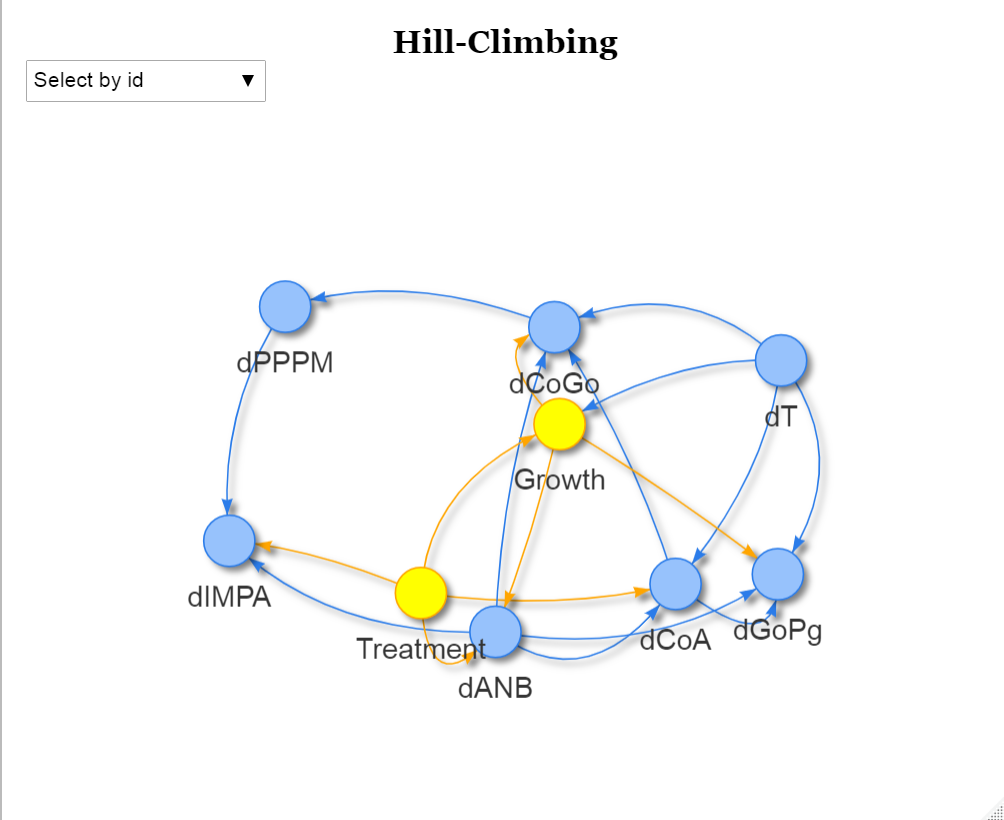
이 함수를 통해 그린 네트워크는 다음과 같습니다. 실제로 R에서 실행하면 interactive plot으로 그려져서 더 보기에 편합니다.

1 2	group = ifelse(names(DAG$nodes)%in%c("Treatment","Growth"),2,1) plot_network(DAG,group=group,title="Hill-Climbing")

Step3: Bootstrapping

Random forest 방법에서 Bagging (Bootstrapping + Aggregating)을 통해 정확도를 향상시키는 것처럼 GBN에서도 한 번만 인과구조를 학습하는 것이 아니라 여러 번 bootstrap sample을 추출해서 각각 인과 구조를 학습하고 이들을 평균내는 방법을 사용합니다. Bootstrap sample은 데이터 크기만큼 추출하되, 반복을 허용합니다. 이 방법을 사용하게 되면 연결의 강도를 알 수 있기 때문에 좋습니다. 이를 하는 방법은 다음과 같습니다.

bnlearn의 boot.strength함수를 통해 bootstrap sample을 추출하고 인과 구조를 학습합니다.
bnlearn의 averaged.network함수를 통해 연결의 강도를 평균냅니다.

strength_diff = boot.strength(diff, R = 200, algorithm = "hc",
                              algorithm.args = list(whitelist = white_list, blacklist = black_list))
head(strength_diff)
attr(strength_diff)
average_diff = averaged.network(strength_diff)

strength_diff의 출력값을 확인해보면 4개의 열을 가지고 있습니다.

> head(strength_diff)
 from    to strength direction
1 dANB dPPPM    0.615 0.2926829
2 dANB dIMPA    1.000 1.0000000
3 dANB  dCoA    0.785 0.5859873
4 dANB dGoPg    0.505 0.7029703
5 dANB dCoGo    0.565 0.8185841
6 dANB    dT    0.130 0.0000000

> attr(strength_diff, "threshold")
[1] 0.505

from과 to는 각각의 edge (arc)
strength는 bootstrap sample에서 순서에 상관없이 from $\rightarrow$ to나 to $\rightarrow$ from의 연결이 나온 확률
direction은 bootstrap sample에서 from $\rightarrow$ to의 연결이 나온 확률

을 의미합니다. 여기서 두 번째 dANB $\rightarrow$ dIMPA의 연결은 strength와 direction이 모두 1이므로 매우 강한 인과 관계를 가지고 있음을 알 수 있죠.

이제 이를 averaged.network()함수에 넣어주면 DAG처럼 네트워크 객체를 만들어줍니다. 다만 strength_diff에서 strength가 임계값 (threshold)를 넘은 edge (arc)들만 추출하여 저장합니다. 여기서 threshold는 0.505로 strength_diff의 6 번째 행인 dANB $\rightarrow$ dT의 연결은 strength가 0.130밖에 되지 않으니 삭제되겠네요!

이제 이 객체를 이용해 네트워크를 그려보았습니다.

1	plot_network(average_diff,strength_diff, group=group)

이제 선의 굵기를 통해서 연결의 강도를 표시할 수 있습니다.

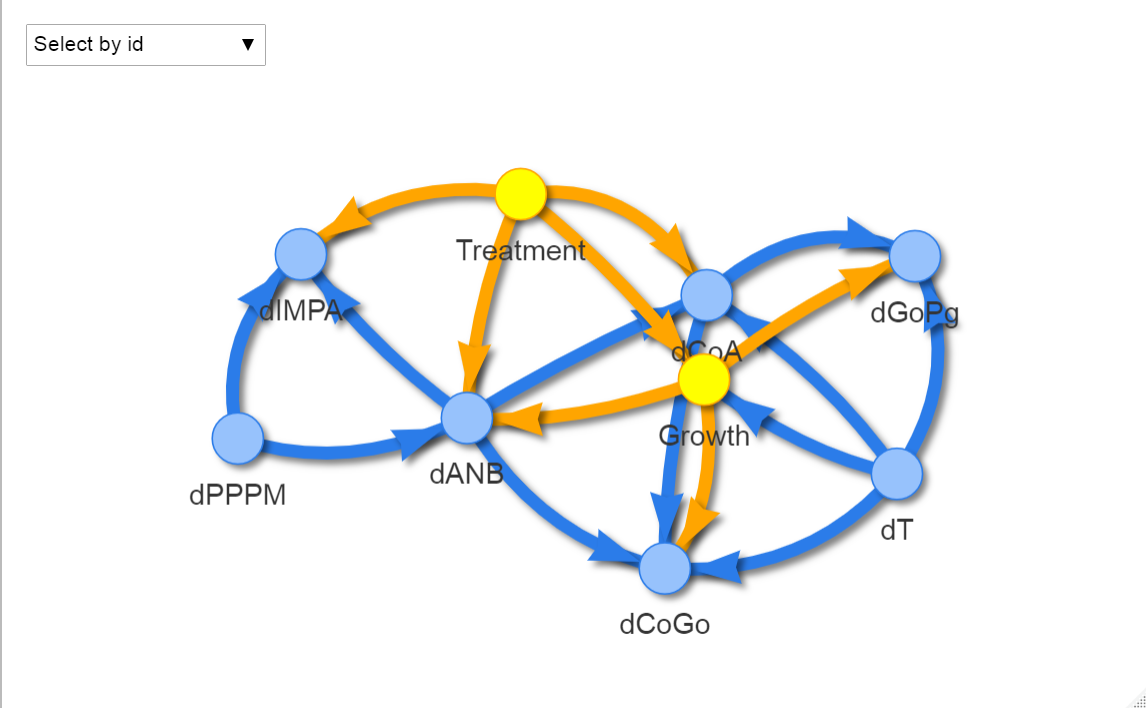
앞서 말씀드렸던 것처럼 dANB $\rightarrow$ dT의 edge는 없는 것을 확인할 수 있습니다.
이보다 그림은 조금 허접하지만 하나만 그린 DAG (single DAG)과 여러 개를 그려 평균을 낸 DAG (averaged DAG)를 graphviz.compare함수를 통해서 확인할 수 있습니다.

1 2	par(mfrow=c(1,2)) graphviz.compare(average_diff, DAG, shape = "ellipse", main = c("averaged DAG", "single DAG"))

여기서 오른쪽에 빨간색, 파란색 선이 single DAG와 averaged DAG의 차이점입니다. 즉 빨간색 선은 single DAG에는 있었으나 averaged DAG에서 사라진 연결, 파란색 선은 single DAG에는 없었으나 averaged DAG에서 생긴 연결을 의미합니다.

Step4: Pruning

사실 이걸 pruning이라고 직접 표현하는 지는 않지만 Regression Tree와 같이 "가지 치기"를 통해 인과 관계를 더 깔끔히 정리할 수 있습니다.
그 방법은 strength_diff의 threshold를 높이는 것입니다.

1
2
3

plot(strength_diff)
abline(v = 0.75, col = "tomato", lty = 2, lwd = 2)
abline(v = 0.85, col = "steelblue", lty = 2, lwd = 2)

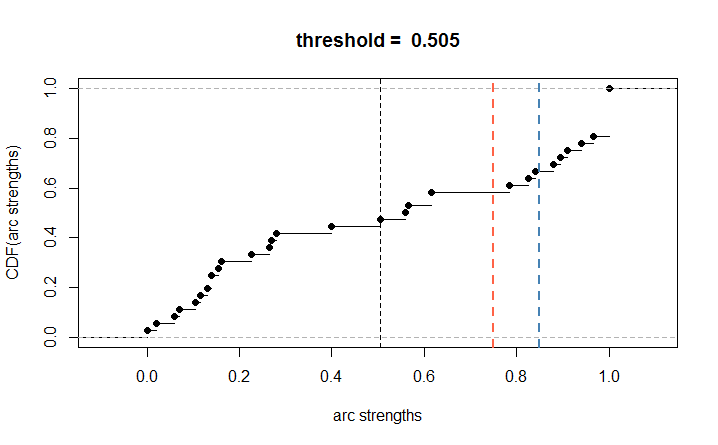
위 그림은 strength_diff의 strength에 따른 CDF를 그린 건데요. 기본 threshold는 아까 확인했듯이 0.505였습니다.
참고로 threshold는 DAG의 CDF가 어떻게 그려지느냐에 따라 다르고, 0.5에 최대한 가깝게 자르는 것 같습니다.

이보다 더 높게 threshold를 0.75 혹은 0.85로 설정하게 되면 더 적은 edge (arc)만 평균 네트워크에 포함되게 됩니다. 아래의 코드를 실행했을 때 알 수 있듯이,
threshold를 0.75로 설정하면 15개, 0.85로 설정하면 12개의 edge (arc)만 포함됩니다.

nrow(strength_diff[strength_diff$strength > 0.75 & strength_diff$direction > 0.5, ])
[1] 15
nrow(strength_diff[strength_diff$strength > 0.85 & strength_diff$direction > 0.5, ])
[1] 12

threshold=0.85로 설정해 다시 평균 네트워크를 그려보았습니다.

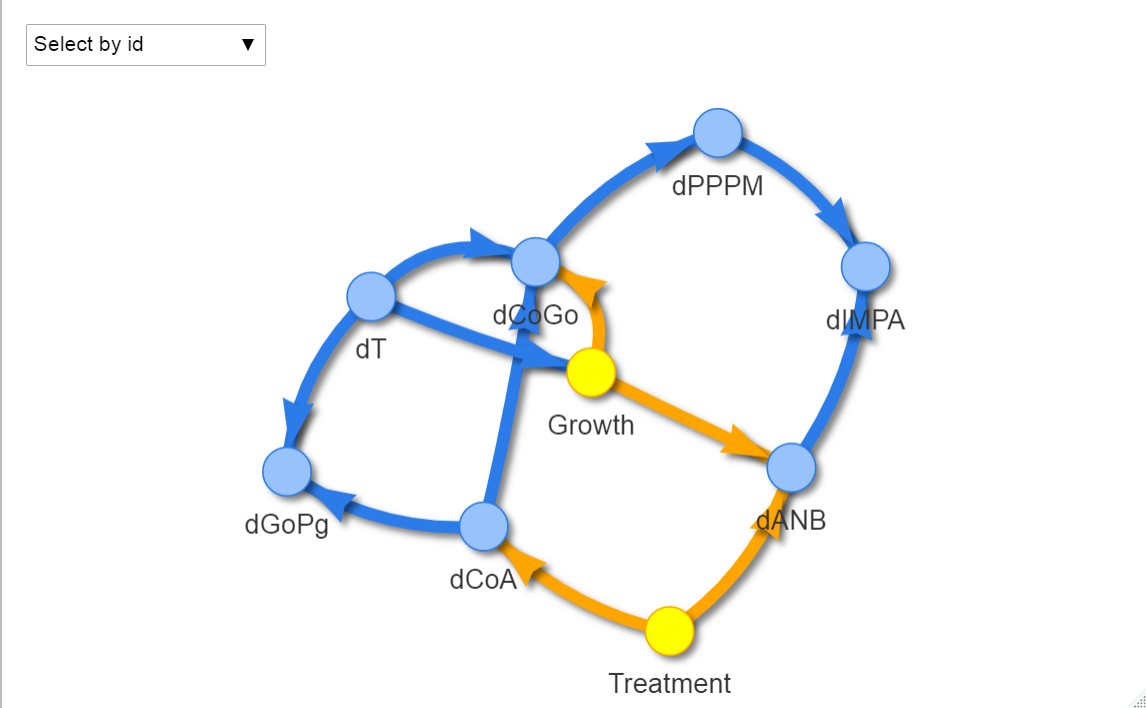
1 2	average_diff_simple = averaged.network(strength_diff, threshold = 0.85) plot_network(average_diff_simple,strength_diff, group=group)

연결의 개수를 세보면 12개임을 확인할 수 있습니다. 이제 이 인과구조로 모수를 추정할겁니다!

Step5: Parameters Learning

모수 추정은 bnlearn::bn.fit을 이용합니다.

1	fit = bn.fit(average_diff_simple, diff)

fit객체는 각 노드마다 회귀식의 결과를 저장하고 있습니다. 여기서 추정 결과는 어떻게 될까요? 위에서 말씀드렸듯이 직계 부모들을 설명 변수에 넣은 회귀식입니다.

예를 들어 dANB는 Treatment와 Growth에 dependent하기 때문에 Treatment와 Growth가 설명 변수로 들어간 선형 회귀식을 적합합니다.

> fit$dANB
Parameters of node dANB (Gaussian distribution)

Conditional density: dANB | Growth + Treatment
Coefficients:
(Intercept)       Growth    Treatment  
  -1.560045     1.173979     1.855994  
Standard deviation of the residuals: 1.416369

> lm(dANB~Growth+Treatment, diff)

Call:
lm(formula = dANB ~ Growth + Treatment, data = diff)

Coefficients:
(Intercept)       Growth    Treatment  
     -1.560        1.174        1.856

이처럼 dANB의 베이지안 네트워크 학습 결과는 직계부모 Growth와 Treatment를 포함한 lm결과와 같음을 확인할 수 있죠.

Step 6: Model Validation

이제 bn.cv함수와 cor-lw를 이용해서 모형의 성능을 평가할 수 있습니다. 자세한 과정은 다음과 같습니다.
cor-lw는 관측값과 예측값의 상관 관계를 구하는 방법으로 target이 범주냐 연속이냐에 따라 평가 방법이 다릅니다.

10-fold cross validation을 10번 (runs=10)시행
각 fold마다 테스트 데이터의 (observed, predicted) 값들을 모음
범주형 변수인 Growth에는 predictive classification error 계산
그 외 연속형 변수에는 predictive correlation 계산

# 10-fold cross validation, # of runs = 10 총 100개
xval = bn.cv(diff, bn = "hc", 
             algorithm.args = list(blacklist = black_list, whitelist = white_list),
             loss = "cor-lw", 
             loss.args = list(target = "Growth", n = 200), 
             runs = 10)

잠깐, GBN은 노드가 모두 연속형인 변수에 쓴다고 했는데, Growth를 정작 평가할 때는 "범주형"으로 쓰나요?

GBN의 가정처럼 Growth변수가 비록 0과 1의 범주형 변수지만 이를 연속형 변수로 간주해서 인과 모형을 적합했습니다.
이게 다범주라면 문제가 되겠지만 2개의 범주만 가지고 있기 때문에 큰 상관은 없죠! (마치 회귀분석에서 dummy 변수를 넣듯이 말입니다)

그러나 평가를 할 때는 예측값이 0.58, 0.62 이런 식으로 연속형으로 나오면 곤란하니, 예측값을 마치 "Growth가 1일 확률"처럼 생각해서 0.5보다 크면 1, 0.5보다 작으면 0으로 범주화해 error를 계산했습니다. 다음과 같이요!

err = numeric(10)
for (i in 1:10){
    tt = table(unlist(sapply(xval[[i]], '[[', "observed")),
               unlist(sapply(xval[[i]], '[[', "predicted")) > 0.50)
    err[i] = (sum(tt) - sum(diag(tt))) / sum(tt)
}

> round(err,3)
 [1] 0.308 0.252 0.259 0.308 0.273 0.280 0.294 0.280 0.301 0.238

err을 보시면 한 fold마다 계산된 오분류율 (misclassification error)를 보여줍니다. 이들의 평균은 0.279로 나옵니다.

두 번째로, Growth를 제외한 연속형 변수에 대해 모형 평가를 해보겠습니다. black list에 따라 dT와 Treatment는 결과가 될 수 없으니 제외했습니다.

# for numeric variable
predcor = structure(numeric(6),names = c("dCoGo", "dGoPg", "dIMPA", "dCoA", "dPPPM", "dANB"))

for (var in names(predcor)) {
    xval = bn.cv(diff, bn = "hc", algorithm.args = list(blacklist = black_list, whitelist = white_list),
                 loss = "cor-lw", loss.args = list(target = var, n = 200), runs = 10)
    predcor[var] = mean(sapply(xval, function(x) attr(x, "mean")))
}

> round(predcor, digits = 3)
dCoGo dGoPg dIMPA  dCoA dPPPM  dANB 
0.851 0.905 0.230 0.925 0.409 0.641

predcor에 저장된 값들은 관측값과 예측값의 평균 상관 관계를 보여줍니다. 앞에서 구한 err와 달리 높을수록 좋죠.
dGoPg와 dCoA는 이 값이 높은 반면, dPPPM은 좀 낮은 편이네요.

Step 7: Intervention

제가 생각하기엔 Intervention이 Bayesian network의 핵심입니다. GBN의 목적은

기존에 가졌던 가정과 인과 관계 결과가 일치하는 지
"만약 이 변수가 이 값을 가졌다면 처리 효과는 어떻게 될까?"와 같은 인과 관계 추정

이기 때문입니다. 직접 관찰한 건 아니지만 인과 관계를 파악하고, 회귀모형을 적합했으니 "만약 $x$ 가 이 값이면 $y$ 가 어떤 값을 가질까?"가 더 정확히 추정되는 것이죠. 이전 포스팅에서 말씀드렸듯이 Bayesian network는 "do-calculus"의 $p(y\vert do(x))$ 를 확인할 수 있다는 장점이 있습니다.
직접 하나의 조건부 확률을 구하려면 bnlearn::cpquery함수를, $p(y\vert do(x))$ 의 난수를 생성하려면 bnlearn::cpdist라는 함수를 씁니다.

Scutari et al. (2017)는 총 6개의 메인 결과를 리포트하고 cpdist함수를 씁니다.
이 중 2개만 추려 말씀드리겠습니다.

1. Treatment를 0으로 고정시켰을 때, CoGo가 급격히 증가하면 PPPM는 감소한다.

sim = cpdist(fit, nodes = c("dCoGo", "dPPPM"), n = 10^4, evidence = (Treatment < 0.5))
nrow(sim) #5332
plot(sim, col = "grey")
abline(v = 0, col = 2, lty = 2, lwd = 2)
abline(h = 0, col = 2, lty = 2, lwd = 2)
abline(coef(lm(dPPPM ~ dCoGo, data = sim)), lwd = 2)

코드에서 evidence는 Intervention에 해당합니다! 즉, 가정의 조건인 Treatment를 0으로 고정시킨 것을 의미합니다.
근데 sim에서 보면 10,000개의 난수를 생성했는데 실제 생성된 난수의 개수는 5,332개로 나왔습니다. 이상하지 않나요? ㅎㅎ
베이지안 방식에서 알려지지 않은 분포에서 난수를 생성하기 위해 쓰는 "Rejection algorithm"을 쓰기 때문에 10,000개의 난수가 모두 쓰이지 않고
채택된 난수만 저장되기 때문입니다.

본론으로 돌아와, Treatment를 0으로 두었을 때 dCoGo와 dPPPM의 난수가 생성되었고 이를 산점도를 통해 그려보았습니다.

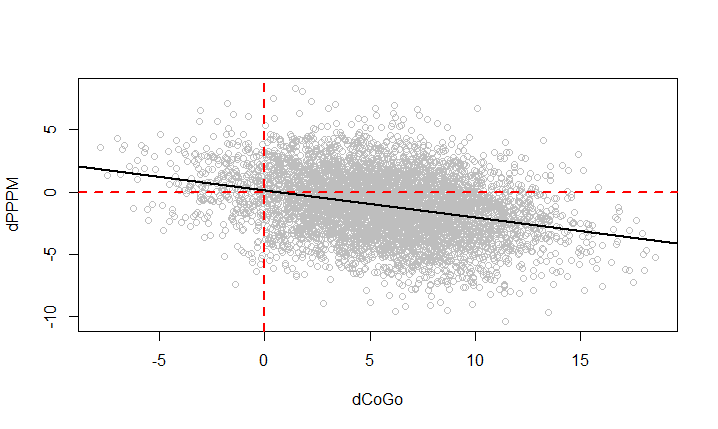
Treatment를 0으로 두었을 때, dCoGo가 증가하면 dPPM이 감소하는 경향이 확실히 보이죠! 따라서 기존의 가정과 인과관계 추정 결과가 일치함을 알 수 있습니다.

2. Treatment의 목적은 ANB이 줄어드는 것을 막는 것이다. 만약 GoPg의 값을 낮게 유지한다면 치료받은 환자와 받지 못한 환자의 ANB에 차이가 있을까?

sim6 = cpdist(fit, nodes = c("Treatment", "dANB", "dGoPg"),
           n=10^5,
           evidence = abs(dGoPg) < 0.1)

sim6$Treatment = ifelse(sim6$Treatment>0.5, 1, 0)
boxplot(dANB ~ Treatment, data = sim6)

마찬가지로 코드에서 evidence인 GoPg의 차이 (dGoPg)의 절대값을 0.1 미만으로 두는 것이 intervention입니다. 이 가정 하에 Treatment의 효과가 있을까? 하고 보는 것이 목적인데요.

위의 boxplot을 보듯이 Treatment를 받았을 때 dANB 값이 더 높고, 양수임을 확인할 수 있죠? 따라서 ANB의 차이가 양수니까, T2시점에서 ANB 값이 더 커졌음을 의미하네요.

What’s Next?

저도 Causal inference 중 Bayesian network 쪽은 처음 공부해봤는데요. 생각보다(?) 과정이 간단함을 느꼈습니다. 베이즈 정리의 기본이 되는 조건부 확률만 알아도 이해하기가 수월하다 생각이 듭니다. GBN을 다시 한 번 정리하자면 조건부 확률을 이용해 인과 구조를 학습하고, 구조를 바탕으로 모수를 선형 회귀를 통해 추정하는 방식입니다.

구조를 학습하는 방법으로 Hill-climbing은 연결을 각각 수정해보면서 BIC와 같은 점수를 비교하고, Grow-Shrink Markov Blanket은 노드마다 Markov blanket을 찾기 위한 여정으로 성장과 축소단계를 거칩니다. 이후 모수를 추정하기 위해 종속 관계 (dependency)를 바탕으로 선형 회귀를 적용합니다.

이 글을 정리하며 궁금했던 점은

꼭 선형 회귀로 모수를 추정해야 하는 지? 다른 advanced 방법은 있는 지?
노드가 100개 이상 넘어갈 때 잘 작동할까?

입니다. 이에 대한 research가 더 필요할 것 같네요 😃 이와 더불어 Potential outcomes 방법론들에 대해서도 정리하고 싶습니다.

References

R 패키지 bnlearn tutorial [link]
R 패키지 visNetwork tutorial[link]
D. Margaritis (2003), Learning Bayesian Network Model Structure from Data. PhD thesis, School of Computer Science, Carnegie-Mellon University, Pittsburgh, PA, Available as Technical Report CMU-CS-03-153. [pdf]
Scutari, M., Auconi, P., Caldarelli, G., & Franchi, L. (2017). Bayesian networks analysis of malocclusion data. Scientific reports, 7(1), 1-11. [pdf]